
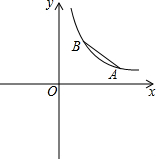
 如图.反比例函数y=$\frac{k}{x}$在第一象限内的图象上有点A、B,已知点A(3m.m)、点B(n,n+1)(其中m>0,n>0).
如图.反比例函数y=$\frac{k}{x}$在第一象限内的图象上有点A、B,已知点A(3m.m)、点B(n,n+1)(其中m>0,n>0).分析 (1)如图1,作辅助线,构建直角△AOC,利用勾股定理求出m的值,写出点A的坐标,由此求出反比例函数的解析式,再求点B的坐标;
(2)有两种情况:过A、B分别作AB的垂线,得到两个矩形,作辅助线,构建直角三角形,证明△ADB≌△M2EN2和△BGM2≌△N2FA,求出OM2、OM1的长,并根据线段的长写出坐标,注意象限的符号问题.
解答 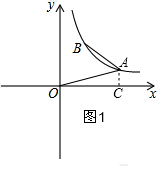 解:(1)如图1,过A作AC⊥x轴于C,
解:(1)如图1,过A作AC⊥x轴于C,
∵点A(3m.m)、且A在第一象限,
∴AC=m,OC=3m,
∵OA=2$\sqrt{10}$,
由勾股定理得:${m}^{2}+(3m)^{2}=(2\sqrt{10})^{2}$,
m=±2,
∵m>0,
∴m=2,
∴A(6,2),
∴k=6×2=12,
∴反比例函数解析式为:y=$\frac{12}{x}$;
∵点B(n,n+1)在反比例函数y=$\frac{k}{x}$的图象上,
∴n(n+1)=12,
n2+n-12=0,
(n+4)(n-3)=0,
n=-4或3,
∵n>0,
∴n=3,
∴B(3,4);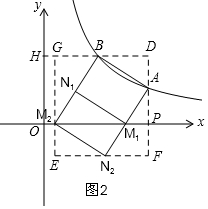
(2)如图2,过N2作EF∥x轴,过A作DF⊥x轴,过M2作M2E⊥x轴,过B作BD∥x轴,分别交于E、F、D、G四点,
∵A(6,2),B(3,4),
∴AD=4-2=2,BD=6-3=3,
∵四边形ABM2N2是矩形,
∴∠M2BA=∠M2N2A=∠BAN2=90°,AB=M2N2,
∴∠M2N2E+∠AN2F=90°,∠N2AF+∠AN2F=90°,
∴∠M2N2E=∠N2AF,
同理得:∠M2N2E=∠ABD,
∵∠M2EN2=∠BDA=90°,
∴△ADB≌△M2EN2,
∴M2E=AD=2,N2E=BD=3,
同理△BGM2≌△N2FA,
∴M2G=AF=4,BG=FN2,
∵∠M2GB=∠ADB=90°,∠GM2B=∠ABD,
∴△BDA∽△M2GB,
∴$\frac{BD}{{M}_{2}G}$=$\frac{AD}{BG}$,
∴$\frac{3}{4}=\frac{2}{BG}$,
∴BG=$\frac{8}{3}$,
∴GH=OM2=BH-BG=3-$\frac{8}{3}$=$\frac{1}{3}$,
∴M2($\frac{1}{3}$,0),N2(3+$\frac{1}{3}$=$\frac{10}{3}$,-2),
∵AP=PF=2,
∴P是AF的中点,
∴PM1△AFN2的中位线,
∴M1P=$\frac{1}{2}F{N}_{2}$=$\frac{1}{2}$BG=$\frac{1}{2}$×$\frac{8}{3}$=$\frac{4}{3}$,
∴OM1=OP-M1P=6-$\frac{4}{3}$=$\frac{14}{3}$,
∴M1($\frac{14}{3}$,0),
∵△M2N2M1≌△M1N1M2,
∴N1($\frac{14}{3}$-3,2)即N1($\frac{5}{3}$,2).
综上所述,M1($\frac{14}{3}$,0),N1($\frac{5}{3}$,2)或M2($\frac{1}{3}$,0),N2($\frac{10}{3}$,-2).
点评 本题考查了矩形的性质和判定、利用待定系数法求反比例函数的解析式,利用三角形全等和相似求出对应的线段的长,同时还采用了分类讨论的思想,要证明两三角形相似和全等时,运用了同角的余角相等证明两个角相等,这在图形有直角的几何题中经常运用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=0,b=1 | B. | a=1,b=0 | C. | a=0,b=0 | D. | a=1,b=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
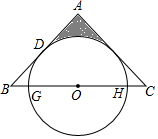 如图,已知△ABC为等腰三角形,点O是底边BC上中点,腰AB与⊙O相切于点D.
如图,已知△ABC为等腰三角形,点O是底边BC上中点,腰AB与⊙O相切于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
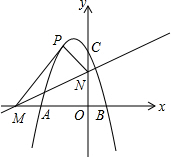 如图,抛物线y=-x2-2x+3与x轴交于A,B两点,与x轴交于C点,直线y=$\frac{1}{2}$x+m交x轴于M,交y轴于N,将△MON沿直线MN折叠,得到△MPN,若点P恰好落在第一象限的抛物线上,求点P的坐标及m的值.
如图,抛物线y=-x2-2x+3与x轴交于A,B两点,与x轴交于C点,直线y=$\frac{1}{2}$x+m交x轴于M,交y轴于N,将△MON沿直线MN折叠,得到△MPN,若点P恰好落在第一象限的抛物线上,求点P的坐标及m的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com