[题目]如图.从点A(0,4)出发的一束光.经x轴反射.过点C(6,4).求这束光从点A到点C所经过的路径长度. 题目和参考答案——青夏教育精英家教网—

【题目】如图，从点A(0,4)出发的一束光，经x轴反射，过点C(6,4)，求这束光从点A到点C所经过的路径长度.

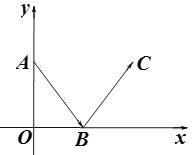
【答案】10.

【解析】

首先过点B作BD⊥x轴于D，由A（0，4），C(6,4)，即可得OA = CD = 4，OD = 6，由题意易证得△AOB≌△CDB，根据全等三角形即可得OB = BD = 3，AB = CB，又由勾股定理即可求得这束光从点A到点C所经过的路径的长．

解：如图，过点C作CD⊥x轴于点D，

∵A(0,4)，C(6,4)，

∴OA = CD = 4，OD = 6，

由题意得，∠ABO =∠CBD,

∵∠AOB =∠CDB =90°，

∴△AOB≌△CDB，

∴OB = BD = 3，AB = CB,

在Rt△AOB中，,

∴这束光从点A到点C所经过的路径长度为AB+BC=10.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，直线l：y＝x+1交x轴于点A，交y轴于点A1，A2，A3，…在直线l上，点B1，B2，B3…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形AnBn﹣1Bn，顶点Bn的坐标为_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB=AC=10厘米，∠B=∠C，BC=8厘米，点D为AB的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，当一个点停止运动时，另一个点也随之停止运动，当点Q的运动速度为时，能够在某一时刻使△BPD与△CQP全等．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】新知识一般有两类：第一类是一般不依赖于其他知识的新知识，如“数”，“字母表示数”这样的初始性知识；第二类是在某些旧知识的基础上联系，拓展等方式产生的知识，大多数知识是这一类．

（1）多项式乘多项式的法则，是第几类知识？

（2）在多项式乘多项式之前，我们学习了哪些有关的知识？（写出三条即可）

（3）请你用已有的知识，从数和形两个方面说明多项式乘多项式法则，用（a+b）（a-b）来说明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为弘扬中华传统文化，我市某中学决定根据学生的兴趣爱好组建课外兴趣小组，因此学校随机抽取了部分同学的兴趣爱好进行调查，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：

（1）学校这次调查共抽取了　　名学生；

（2）补全条形统计图；

（3）在扇形统计图中，“戏曲”所在扇形的圆心角度数为　　；

（4）设该校共有学生2000名，请你估计该校有多少名学生喜欢书法？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在BC边所在直线上， PE＝PB．

(1)如图1，当点E在线段BC上时，

求证：①PE＝PD，②PE⊥PD.

简析：由正方形的性质，图1中有三对全等的三角形，

即△ABC≌△ADC，_______≌_______，和_______≌______，由全等三角形性质，结合条件中PE＝PB，易证PE＝PD.要证PE⊥PD，考虑到∠ECD = 90°，故在四边形PECD中，只需证∠PDC +∠PEC＝______即可.再结合全等三角形和等腰三角形PBE的性质，结论可证.