
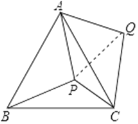
【题目】P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=________.
【答案】3:4:2
【解析】
将△APB绕A点逆时针旋转60![]() 得△AQC,显然有△AQC≌△APB,连PQ ,可得△AQP是等边三角形,△QCP的三边长分别为PA,PB,PC ,由∠APB+∠BPC+∠CPA=360
得△AQC,显然有△AQC≌△APB,连PQ ,可得△AQP是等边三角形,△QCP的三边长分别为PA,PB,PC ,由∠APB+∠BPC+∠CPA=360![]() ,∠APB: ∠BPC: ∠CPA=5:6:7,可得∠APB=100
,∠APB: ∠BPC: ∠CPA=5:6:7,可得∠APB=100![]() , ∠BPC=120
, ∠BPC=120![]() , ∠CPA=140
, ∠CPA=140![]() ,可得答案.
,可得答案.
解:如图, 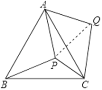
将△APB绕A点逆时针旋转60![]() 得△AQC,显然有△AQC≌△APB,连PQ,
得△AQC,显然有△AQC≌△APB,连PQ,
![]() AQ=AP,∠QAP=60
AQ=AP,∠QAP=60![]() ,
,
![]() △AQP是等边三角形,
△AQP是等边三角形,
![]() PQ=AP,
PQ=AP,
![]() QC=PB,
QC=PB,![]() △QCP的三边长分别为PA,PB,PC,
△QCP的三边长分别为PA,PB,PC,
![]() ∠APB+∠BPC+∠CPA=360
∠APB+∠BPC+∠CPA=360![]() ,∠APB: ∠BPC: ∠CPA=5:6:7,
,∠APB: ∠BPC: ∠CPA=5:6:7,
![]() ∠APB=100
∠APB=100![]() , ∠BPC=120
, ∠BPC=120![]() , ∠CPA=140
, ∠CPA=140![]() ,
,
![]() ∠PQC=∠AQC-∠AQP=∠APB-∠AQP=100
∠PQC=∠AQC-∠AQP=∠APB-∠AQP=100![]() -60
-60![]() =40
=40![]() ,
,
∠QPC=∠APC-∠APQ=140![]() -60
-60![]() =80
=80![]() ,
,
∠PCQ=180![]() -(40
-(40![]() +80
+80![]() )=60
)=60![]() ,
,
![]() ∠PCQ: ∠QPC: ∠PQC=3:4:2,
∠PCQ: ∠QPC: ∠PQC=3:4:2,
故答案为:3:4:2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
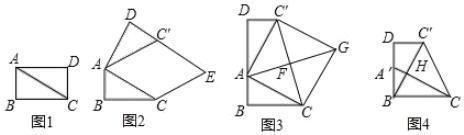
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如 图 1,将:矩形纸片 ABCD 沿对角线 AC 剪开,得到△ABC 和△ACD.并且量得 AB =4cm,AC=8cm.
操作发现:
(1)将图 1 中的△ACD 以点 A 为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到如图 2 所示的△AC′D,过点 C 作 AC′的平行线,与 DC'的延长线 交于点 E,则四边形 ACEC′的形状是 .
(2)创新小组将图 1 中的△ACD 以点 A 为旋转中心,按逆时针方向旋转,使 B、 A、D 三点在同一条直线上,得到如图 3 所示的△AC′D,连接 CC',取 CC′的中 点 F,连接 AF 并延长至点 G,使 FG=AF,连接 CG、C′G,得到四边形 ACGC′, 发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC 沿着 BD 方向平移,使点 B 与点 A 重合,此时 A 点平移至 A'点,A'C 与 BC′相交于点 H, 如图 4 所示,连接 CC′,试求 tan∠C′CH 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2+(1﹣2m)x+1﹣3m.
(1)当m=2时,求二次函数图象的顶点坐标;
(2)已知抛物线与x轴交于不同的点A、B.
①求m的取值范围;
②若3≤m≤4时,求线段AB的最大值及此时二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受到“新型肺炎”影响,全国中小学未能按时开学,为响应国家“停课不停学”的号召,重庆某重点中学组织全校师生开展线上教学活动,体育备课组也为同学们提出了每日锻炼建议.疫情过去开学后,体育组彭老师为检测同学们在家锻炼情况,在甲、乙两班同学中各随机抽取![]() 名学生进行检测,并对数据进行了整理、分析.下面给出了部分信息:
名学生进行检测,并对数据进行了整理、分析.下面给出了部分信息:
甲班![]()
乙班成绩在![]() 中的数据是
中的数据是![]()
整理数据:
成绩 班级 |
|
|
|
|
甲 |
|
|
|
|
乙 |
|
|
|
|
分析数据:
班级 | 平均数 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]()
![]()
![]()
![]() 根据以上数据,你认为哪个班级在家体育锻炼的效果比较好,请说明理由(
根据以上数据,你认为哪个班级在家体育锻炼的效果比较好,请说明理由(![]() 条理由即可).
条理由即可).
![]() 已知九年级共有
已知九年级共有![]() 名学生,请估计全年级体育成绩大于等于
名学生,请估计全年级体育成绩大于等于![]() 分的学生有多少人?
分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
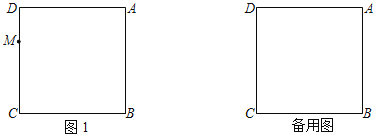
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
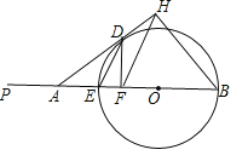
【题目】已知,如图,EB是![]() 的直径,且
的直径,且![]() ,在BE的延长线上取点P,使
,在BE的延长线上取点P,使![]() ,A是EP上一点,过A作
,A是EP上一点,过A作![]() 的切线,切点为D,过D作
的切线,切点为D,过D作![]() 于F,过B作AD的垂线BH,交AD的延长线于
于F,过B作AD的垂线BH,交AD的延长线于![]() 当点A在EP上运动,不与E重合时:
当点A在EP上运动,不与E重合时:
![]() 是否总有
是否总有![]() ,试证明你的结论;
,试证明你的结论;
![]() 设
设![]() ,
,![]() ,求y和x的函数关系,并写出x的取值范围.
,求y和x的函数关系,并写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com