
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC关于原点O成中心对称的△A2B2C2;
(2)求△A2B2C2的面积.
【答案】
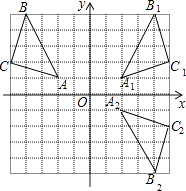
(1)解:①如图,△A1B1C1为所作
②如图,△A2B2C2为所作
(2)解:△A2B2C2的面积=3×4﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×3﹣
×3﹣ ![]() ×4×2=5
×4×2=5
【解析】(1)①利用关于y轴对称的点的坐标特征写出A、B、C关于y轴的对称点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;②利用关于原点对称的点的坐标特征写出A、B、C关于y轴的对称点A2、B2、C2的坐标,然后描点即可得到△A2B2C2;(2)利用一个矩形的面积分别减去三个三角形的面积可计算出△A2B2C2的面积.
【考点精析】通过灵活运用作轴对称图形,掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线即可以解答此题.


科目:初中数学 来源: 题型:
【题目】(1)如图,一个直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C,△ABC中,若∠A=30°,则∠ABC+∠ACB=__ __,∠XBC+∠XCB=__ __;
(2)若改变直角三角板XYZ的位置,但三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) 
A.①②
B.②③
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
(2)【类比探究】
如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(3)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC. 
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师驾车从家出发到植物园赏花,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后加速行驶,到达植物园,参观结束后,张老师驾车一路匀速返回,其中x表示汽车从家出发后所用时间,y表示车离家的距离,下面能反映y与x的函数关系式的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com