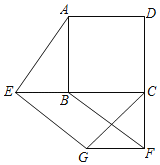
【题目】如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE=CF，过点E作FG∥BF，交正方形外角的平分线CG于点G，连接GF．求证：
（1）AE⊥BF；
（2）四边形BEGF是平行四边形．
科目：初中数学 来源： 题型：
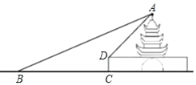
【题目】在一次数学综合实践活动中，小明计划测量城门大楼的高度，在点B处测得楼顶A的仰角为22°，他正对着城楼前进21米到达C处，再登上3米高的楼台D处，并测得此时楼顶A的仰角为45°．
（1）求城门大楼的高度；
（2）每逢重大节日，城门大楼管理处都要在A，B之间拉上绳子，并在绳子上挂一些彩旗，请你求出A，B之间所挂彩旗的长度（结果保留整数）．（参考数据：sin22°≈
，cos22°≈
，tan22°≈
）
查看答案和解析>>
科目：初中数学 来源： 题型：
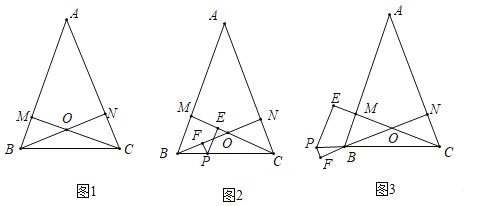
【题目】在等腰三角形
中，
，作
交AB于点M，
交AC于点N．
（1）在图1中，求证：
；
（2）在图2中的线段CB上取一动点P，过P作
交CM于点E，作
交BN于点F，求证：
；
（3）在图3中动点P在线段CB的延长线上，类似（2）过P作交CM的延长线于点E，作交NB的延长线于点F，求证：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某出租公司有若干辆同一型号的货车对外出租，每辆货车的日租金实行淡季、旺季两种价格标准，旺季每辆货车的日租金比淡季上涨
．据统计，淡季该公司平均每天有
辆货车未出租，日租金总收入为
元；旺季所有的货车每天能全部租出，日租金总收入为
元．
（1）该出租公司这批对外出租的货车共有多少辆？淡季每辆货车的日租金多少元？
（2）经市场调查发现，在旺季如果每辆货车的日租金每上涨
元，每天租出去的货车就会减少
辆，不考虑其它因素，每辆货车的日租金上涨多少元时，该出租公司的日租金总收入最高？
查看答案和解析>>
科目：初中数学 来源： 题型：
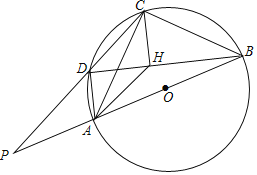
【题目】四边形
是
的圆内接四边形，线段
是的直径，连结
．点
是线段
上的一点，连结
，且
，
的延长线与
的延长线相交与点
．
（1）求证：四边形
是平行四边形；
（2）若
，
①求证：
为等腰直角三角形；
②求
的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的袋子中装有四个小球，上面分别标有数字-2，-1，0，1，它们除了数字不一样外，其它完全相同.
（1）随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是__________.
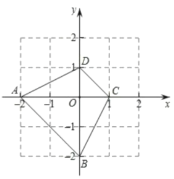
（2）小聪先从袋子中随机摸出一个小球，记下数字作为点
的纵坐标，如图，已知四边形
的四个顶点的坐标分别为
，
，
，
，请用画树状图或列表法，求点落在四边形所围成的部分内（含边界）的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
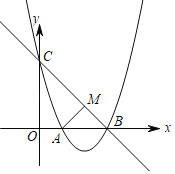
【题目】已知抛物线
过点
，
两点，与y轴交于点C，
．
(1)求抛物线的解析式及顶点D的坐标；
(2)过点A作
，垂足为M，求证：四边形ADBM为正方形；
(3)点P为抛物线在直线BC下方图形上的一动点，当
面积最大时，求点P的坐标；
(4)若点Q为线段OC上的一动点，问：
是否存在最小值？若存在，求岀这个最小值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解七、八年级学生一分钟跳绳情况，从这两个年级随机抽取
名学生进行测试，并对测试成绩（一分钟跳绳次数）进行整理、描述和分析，下面给出了部分信息：
七年级学生一分钟跳绳成绩频数分布直方图
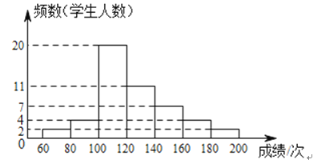
七、八年级学生一分钟跳绳成绩分析表
七年级学生一分钟跳绳成绩（数据分
组：
）在
这一组的是：
根据以上信息，回答下列问题：
表中
；
在这次测试中，七年级甲同学的成绩
次，八年级乙同学的成绩
，他们的测试成绩，在各自年级所抽取的名同学中，排名更靠前的是 （填“甲”或“乙”），理由是 ．
该校七年级共有
名学生，估计一分钟跳绳不低于次的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
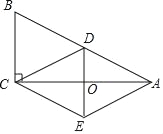
【题目】如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，AE∥CD，CE∥AB，连接DE交AC于点O．
（1）证明：四边形ADCE为菱形．
（2）BC＝6，AB＝10，求菱形ADCE的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
