
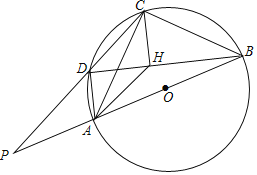
【题目】四边形![]() 是
是![]() 的圆内接四边形,线段
的圆内接四边形,线段![]() 是
是![]() 的直径,连结
的直径,连结![]() .点
.点![]() 是线段
是线段![]() 上的一点,连结
上的一点,连结![]() ,且
,且![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线相交与点
的延长线相交与点![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]()
①求证:![]() 为等腰直角三角形;
为等腰直角三角形;
②求![]() 的长度.
的长度.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
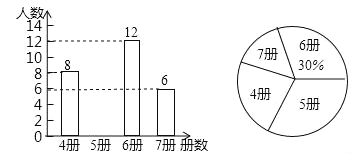
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
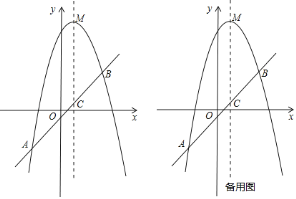
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ),
),![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
(4)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
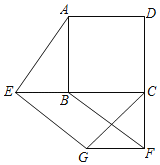
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作FG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
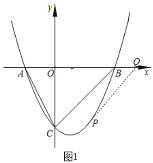
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,线段
的坐标为__________,线段![]() 的长为__________,抛物线的解析式为__________.
的长为__________,抛物线的解析式为__________.
(2)点![]() 是线段
是线段![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
①如果在![]() 轴上存在点
轴上存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.求点
为顶点的四边形是平行四边形.求点![]() 的坐标.
的坐标.
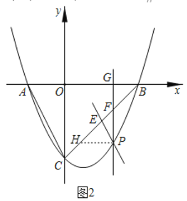
②如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,记
,记![]() ,求
,求![]() 关于
关于![]() 的函数解析式;当
的函数解析式;当![]() 取
取![]() 和
和![]() 时,试比较
时,试比较![]() 的对应函数值
的对应函数值![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
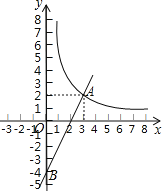
(1)求函数![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)结合图象直接写出不等式组0<![]() <kx+b的解集.
<kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com