
【题目】如图1,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
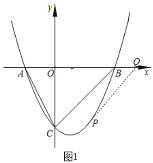
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,线段
的坐标为__________,线段![]() 的长为__________,抛物线的解析式为__________.
的长为__________,抛物线的解析式为__________.
(2)点![]() 是线段
是线段![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
①如果在![]() 轴上存在点
轴上存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.求点
为顶点的四边形是平行四边形.求点![]() 的坐标.
的坐标.
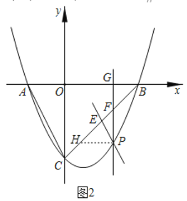
②如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,记
,记![]() ,求
,求![]() 关于
关于![]() 的函数解析式;当
的函数解析式;当![]() 取
取![]() 和
和![]() 时,试比较
时,试比较![]() 的对应函数值
的对应函数值![]() 和
和![]() 的大小.
的大小.
【答案】(1)![]() 、
、![]() 、
、![]() 、
、![]() ;(2)①点
;(2)①点![]() 的坐标为
的坐标为![]() 或
或![]() ;②
;②![]() .
.
【解析】
(1)由题意得:![]() ,故
,故![]() ,即可求解;
,即可求解;
(2)①分![]() 是平行四边形的一条边时、
是平行四边形的一条边时、![]() 是平行四边形的对角线时,两种情况分别求解即可;
是平行四边形的对角线时,两种情况分别求解即可;
②如图,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,证明
,证明![]() ,根据相似三角形的对应边成比例可得
,根据相似三角形的对应边成比例可得![]() ,设点
,设点![]() ,点
,点![]() ,则
,则![]() ,继而可得
,继而可得![]() ,由此即可求得答案.
,由此即可求得答案.
(1)由题意得:![]() ,故
,故![]() ,
,
故抛物线的表达式为:![]() ,
,
令![]() ,则
,则![]() 或
或![]() ,即点
,即点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
则![]() ,
,
故答案为:![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2)①当![]() 是平行四边形的一条边时,
是平行四边形的一条边时,

如图所示,点![]() 向右平移4个单位、向上平移4个单位得到点
向右平移4个单位、向上平移4个单位得到点![]() ,
,
设:点![]() ,点
,点![]() ,
,
则点![]() 向右平移4个单位、向上平移4个单位得到点
向右平移4个单位、向上平移4个单位得到点![]() ,
,
即:![]() ,
,![]() ,
,
解得:![]() 或6(舍去4),
或6(舍去4),
即点![]() ;
;
当![]() 是平行四边形的对角线时,
是平行四边形的对角线时,
设点![]() 、点
、点![]() ,其中
,其中![]() ,
,
由中心公式可得:![]() ,
,![]() ,
,
解得:![]() 或4(舍去4),
或4(舍去4),
故点![]() ;
;
故点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
②如图,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,
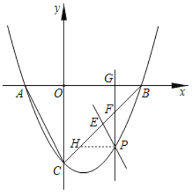
∵![]() 轴,∴
轴,∴![]() ,
,
∵![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,∴
,∴![]() ,即:
,即:![]() ,
,
则![]() ,
,
设点![]() ,点
,点![]() ,
,
则![]() ,
,
则![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
则![]() ,
,
则![]() ,∴
,∴![]() ,
,
![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
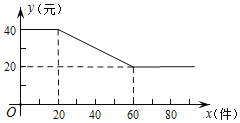
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
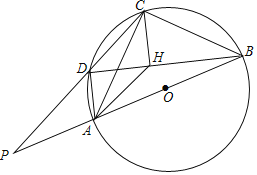
【题目】四边形![]() 是
是![]() 的圆内接四边形,线段
的圆内接四边形,线段![]() 是
是![]() 的直径,连结
的直径,连结![]() .点
.点![]() 是线段
是线段![]() 上的一点,连结
上的一点,连结![]() ,且
,且![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线相交与点
的延长线相交与点![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]()
①求证:![]() 为等腰直角三角形;
为等腰直角三角形;
②求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
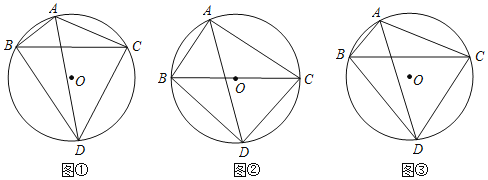
【题目】已知![]() ABC内接于
ABC内接于![]() ,
,![]() 的平分线交
的平分线交![]() 于点D,连接DB,DC.
于点D,连接DB,DC.
(1)如图①,当![]() 时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
(2)如图②,当![]() 时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
(3)如图③,若BC=5,BD=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
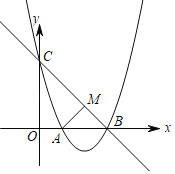
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() 两点,与y轴交于点C,
两点,与y轴交于点C,![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)过点A作![]() ,垂足为M,求证:四边形ADBM为正方形;
,垂足为M,求证:四边形ADBM为正方形;
(3)点P为抛物线在直线BC下方图形上的一动点,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(4)若点Q为线段OC上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高农田利用效益,某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾稻”轮作模式.某农户有农田20亩,去年开始实施“虾稻”轮作,去年出售小龙虾每千克获得的利润为32元(利润=售价﹣成本).由于开发成本下降和市场供求关系变化,今年每千克小龙虾的养殖成本下降25%,售价下降10%,出售小龙虾每千克获得利润为30元.
(1)求去年每千克小龙虾的养殖成本与售价;
(2)该农户今年每亩农田收获小龙虾100千克,若今年的水稻种植成本为600元/亩,稻谷售价为25元/千克,该农户估计今年可获得“虾稻”轮作收入不少于8万元,则稻谷的亩产量至少会达到多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
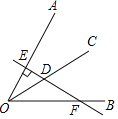
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=![]() (x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).
(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com