
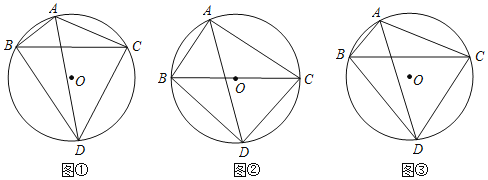
【题目】已知![]() ABC内接于
ABC内接于![]() ,
,![]() 的平分线交
的平分线交![]() 于点D,连接DB,DC.
于点D,连接DB,DC.
(1)如图①,当![]() 时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
(2)如图②,当![]() 时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
(3)如图③,若BC=5,BD=4,求![]() 的值.
的值.
【答案】(1)AB+AC=AD;(2)![]() ;(3)
;(3)![]()
【解析】
(1)在AD上截取AE=AB,连接BE,由条件可知△ABE和△BCD都是等边三角形,可证明△BED≌△BAC,可得DE=AC,则AB+AC=AD;
(2)延长AB至点M,使BM=AC,连接DM,证明△MBD≌△ACD,可得MD=AD,证得AB+AC=![]() ;
;
(3)延长AB至点N,使BN=AC,连接DN,证明△NBD≌△ACD,可得ND=AD,∠N=∠CAD,证△NAD∽△CBD,可得![]() ,
,
可由AN=AB+AC,求出![]() 的值.
的值.
解:(1)如图①在AD上截取AE=AB,连接BE,
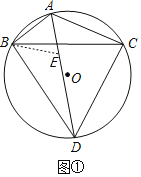
∵∠BAC=120°,∠BAC的平分线交⊙O于点D,
∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,
∴△ABE和△BCD都是等边三角形,
∴∠DBE=∠ABC,AB=BE,BC=BD,
∴△BED≌△BAC(SAS),
∴DE=AC,
∴AD=AE+DE=AB+AC;
故答案为:AB+AC=AD.
(2)AB+AC=![]() .理由如下:
.理由如下:
如图②,延长AB至点M,使BM=AC,连接DM,
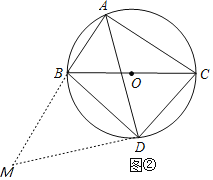
∵四边形ABDC内接于⊙O,
∴∠MBD=∠ACD,
∵∠BAD=∠CAD=45°,
∴BD=CD,
∴△MBD≌△ACD(SAS),
∴MD=AD,∠M=∠CAD=45°,
∴MD⊥AD.
∴AM=![]() ,即AB+BM=
,即AB+BM=![]() ,
,
∴AB+AC=![]() ;
;
(3)如图③,延长AB至点N,使BN=AC,连接DN,
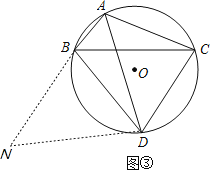
∵四边形ABDC内接于⊙O,
∴∠NBD=∠ACD,
∵∠BAD=∠CAD,
∴BD=CD,
∴△NBD≌△ACD(SAS),
∴ND=AD,∠N=∠CAD,
∴∠N=∠NAD=∠DBC=∠DCB,
∴△NAD∽△CBD,
∴![]() ,
,
∴![]() ,
,
又AN=AB+BN=AB+AC,BC=5,BD=4,
∴![]() .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
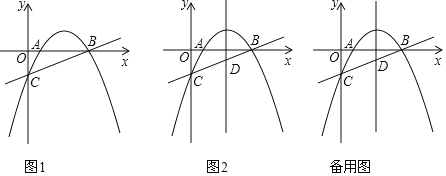
【题目】如图,直线![]() 与x轴、y轴分别交于BC两点,抛物线
与x轴、y轴分别交于BC两点,抛物线![]() 经过B、C两点,且与x轴交于点A
经过B、C两点,且与x轴交于点A
(1)求该抛物线的函数表达式;
(2)已知点M是第一象限内抛物线上的一个动点,过点M作MN平行于y轴交直线BC于点N,连接AM、BM、AN,求四边形MANB面积S的最大值,并求出此时点M的坐标;
(3)抛物线的对称轴交直线BC于点D,若Q为y轴上一点,则在抛物线上是否存在一点P,使得以B、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ),
),![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
(4)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
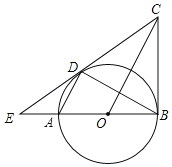
【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
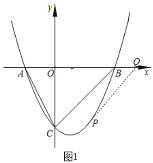
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,线段
的坐标为__________,线段![]() 的长为__________,抛物线的解析式为__________.
的长为__________,抛物线的解析式为__________.
(2)点![]() 是线段
是线段![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
①如果在![]() 轴上存在点
轴上存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.求点
为顶点的四边形是平行四边形.求点![]() 的坐标.
的坐标.
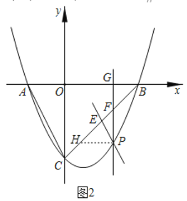
②如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,记
,记![]() ,求
,求![]() 关于
关于![]() 的函数解析式;当
的函数解析式;当![]() 取
取![]() 和
和![]() 时,试比较
时,试比较![]() 的对应函数值
的对应函数值![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
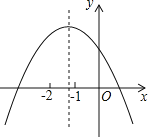
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了迎接“双11”节,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件. 设每件降价x元:
(1)降价后每件利润 元,商场能售出 件.
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com