
【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
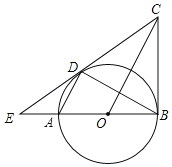
A. 4个B. 3个C. 2个D. 1个
科目:初中数学 来源: 题型:
【题目】在探究“尺规三等分角”这个数学名题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是( )
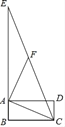
A. 7° B. 21° C. 23° D. 34°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 匀速运动.动点
匀速运动.动点![]() 同时从点
同时从点![]() 出发以同样的速度沿
出发以同样的速度沿![]() 的延长线方向匀速运动,当点
的延长线方向匀速运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 同时停止运动.设运动时间为以
同时停止运动.设运动时间为以![]() .过点
.过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 边于
边于![]() .以
.以![]() 为边作平行四边形
为边作平行四边形![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
(2)是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的平分线上?若存在,求出
的平分线上?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求![]() 的长;
的长;
(4)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,得
翻折,得![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的值最小?并求出最小值.
的值最小?并求出最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强的爸爸准备驾车外出.启动汽车时,车载报警系统显示正前方有障碍物,此时在眼睛点![]() 处测得汽车前端
处测得汽车前端![]() 的俯角为
的俯角为![]() ,且
,且![]() ,若直线
,若直线![]() 与地面
与地面![]() 相交于点
相交于点![]() ,点
,点![]() 到地面
到地面![]() 的垂线段
的垂线段![]() 的长度为1.6米,假设眼睛
的长度为1.6米,假设眼睛![]() 处的水平线
处的水平线![]() 与地面
与地面![]() 平行.
平行.
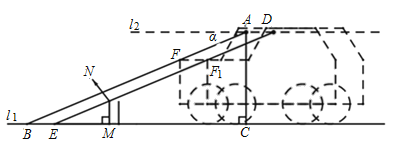
(1)求![]() 的长度;
的长度;
(2)假如障碍物上的点![]() 正好位于线段
正好位于线段![]() 的中点位置(障碍物的横截面为长方形,且线段
的中点位置(障碍物的横截面为长方形,且线段![]() 为此长方形前端的边),
为此长方形前端的边),![]() ,若小强的爸爸将汽车沿直线
,若小强的爸爸将汽车沿直线![]() 后退0.6米,通过汽车的前端
后退0.6米,通过汽车的前端![]() 点恰好看见障碍物的顶部
点恰好看见障碍物的顶部![]() 点(点
点(点![]() 为点
为点![]() 的对应点,点
的对应点,点![]() 为点
为点![]() 的对应点),求障碍物的高度.
的对应点),求障碍物的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ABC内接于
ABC内接于![]() ,
,![]() 的平分线交
的平分线交![]() 于点D,连接DB,DC.
于点D,连接DB,DC.
(1)如图①,当![]() 时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
(2)如图②,当![]() 时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
(3)如图③,若BC=5,BD=4,求![]() 的值.
的值.
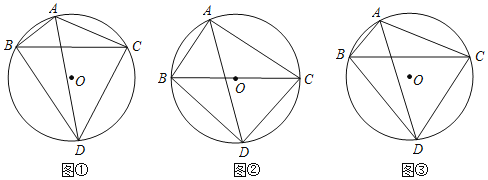
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.
(1)求购买甲、乙两种树苗各多少棵?
(2)为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
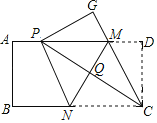
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和直线
和直线![]() 都经过点
都经过点![]() ,点
,点![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线上的动点,直线
为抛物线上的动点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)当![]() 是以
是以![]() 为底边的等腰三角形时,求点
为底边的等腰三角形时,求点![]() 的坐标;
的坐标;
(3)满足(2)的条件时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com