
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЃЉЃЌ
ЃЉЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЌВЂаДГіЫќЕФЖдГЦжсЃЛ
ЃЈ2ЃЉЕу![]() ЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌСЌНг
ЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉвбжЊ![]() ЃЌШє
ЃЌШє![]() ЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЈЦфжа
ЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЈЦфжа![]() ЃЉЃЌСЌНг
ЃЉЃЌСЌНг![]() ЃЌЧѓ
ЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕМАДЫЪБЕу
УцЛ§ЕФзюДѓжЕМАДЫЪБЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ЃЈ4ЃЉШєЕу![]() ЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌХзЮяЯпЩЯЪЧЗёДцдкЕу
ЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌХзЮяЯпЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУвд
ЃЌЪЙЕУвд![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌЖдГЦжс
ЃЌЖдГЦжс![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉУцЛ§газюДѓжЕЪЧ
ЃЛЃЈ3ЃЉУцЛ§газюДѓжЕЪЧ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ4ЃЉДцдкЕу
ЃЛЃЈ4ЃЉДцдкЕу![]() ЪЙЕУвд
ЪЙЕУвд![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌ![]() Лђ
Лђ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
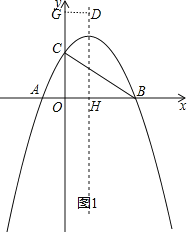
ЃЈ1ЃЉНЋЕуAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉДњШыy=ax2+bx+2МДПЩЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDGЁЭyжсгкGЃЌзїDHЁЭxжсгкHЃЌЩшЕуDЃЈ1ЃЌyЃЉЃЌдкRtЁїCGDжаЃЌCD2=CG2+GD2=ЃЈ2-yЃЉ2+1ЃЌдкRtЁїBHDжаЃЌBD2=BH2+HD2=4+y2ЃЌПЩвджЄУїCD=BDЃЌМДПЩЧѓyЕФжЕЃЛ
ЃЈ3ЃЉЙ§ЕуEзїEQЁЭyжсгкЕуQЃЌЙ§ЕуFзїжБЯпFRЁЭyжсгкRЃЌЙ§ЕуEзїFPЁЭFRгкPЃЌжЄУїЫФБпаЮQRPEЪЧОиаЮЃЌИљОнSЁїCEF=SОиаЮQRPE-SЁїCRF-SЁїEFPЃЌДњШыБпМДПЩЃЛ
ЃЈ4ЃЉИљОнЦНааЫФБпаЮЖдБпЦНааЧвЯрЕШЕФаджЪПЩвдЕУЕНДцдкЕуMЪЙЕУвдBЃЌCЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЕуMЃЈ2ЃЌ2ЃЉЛђMЃЈ4ЃЌ- ![]() ЃЉЛђMЃЈ-2ЃЌ-
ЃЉЛђMЃЈ-2ЃЌ-![]() ЃЉЃЛ
ЃЉЃЛ
НтЃКЃЈ1ЃЉНЋЕу![]() ДњШы
ДњШы![]() ЃЌ
ЃЌ
ПЩЕУ![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
![]() ЖдГЦжс
ЖдГЦжс![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃКЙ§Еу![]() зї
зї![]() жсгк
жсгк![]() ЃЌзї
ЃЌзї![]() жсгк
жсгк![]() ЃЌ
ЃЌ
ЩшЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() дк
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
![]() дк
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]()
![]() ЃЌ
ЃЌ
![]()
![]()
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2ЃКЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() жсгк
жсгк![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гк
гк![]() ЃЌ
ЃЌ

![]() ЃЌ
ЃЌ
![]() ЫФБпаЮ
ЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЕБ
ЕБ![]() ЪБЃЌУцЛ§газюДѓжЕЪЧ
ЪБЃЌУцЛ§газюДѓжЕЪЧ![]() ЃЌ
ЃЌ
ДЫЪБ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉДцдкЕу![]() ЪЙЕУвд
ЪЙЕУвд![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌ
Щш![]() ЃЌ
ЃЌ
ЂйЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЪБЃЌ
ЪЧЦНааЫФБпаЮЪБЃЌ
![]()
![]()
![]()
ЂкЫФБпаЮ![]() ЪБЦНааЫФБпаЮЪБЃЌ
ЪБЦНааЫФБпаЮЪБЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЂлЫФБпаЮ![]() ЪБЦНааЫФБпаЮЪБЃЌ
ЪБЦНааЫФБпаЮЪБЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃК![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЛ
ЃЛ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЃК
ЂйШє![]() ЪЧЭъШЋЦНЗНЪНЃЌдђ
ЪЧЭъШЋЦНЗНЪНЃЌдђ![]() ЃЛ
ЃЛ
ЂкШє![]() Ш§ЕудкЭЌвЛжБЯпЩЯЃЌдђ
Ш§ЕудкЭЌвЛжБЯпЩЯЃЌдђ![]() ЃЛ
ЃЛ
ЂлЕШбќШ§НЧаЮвЛБпЩЯЕФжаЯпЫљдкЕФжБЯпЪЧЫќЕФЖдГЦжсЃЛ
ЂмвЛИіЖрБпаЮЕФФкНЧКЭЪЧЫќЕФЭтНЧКЭЕФ![]() БЖЃЌдђетИіЖрБпаЮЪЧСљБпаЮЃЎ
БЖЃЌдђетИіЖрБпаЮЪЧСљБпаЮЃЎ
ЦфжаецУќЬтИіЪ§ЪЧЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЁЮЂЦѓвЕЮЊМгПьВњвЕзЊаЭЩ§МЖВНЗЅЃЌв§НјвЛХњAЃЌBСНжжаЭКХЕФЛњЦїЃЎвбжЊвЛЬЈAаЭЛњЦїБШвЛЬЈBаЭЛњЦїУПаЁЪБЖрМгЙЄ2ИіСуМўЃЌЧввЛЬЈAаЭЛњЦїМгЙЄ80ИіСуМўгывЛЬЈBаЭЛњЦїМгЙЄ60ИіСуМўЫљгУЪБМфЯрЕШЃЎ
ЃЈ1ЃЉУПЬЈAЃЌBСНжжаЭКХЕФЛњЦїУПаЁЪБЗжБ№МгЙЄЖрЩйИіСуМўЃП
ЃЈ2ЃЉШчЙћИУЦѓвЕМЦЛЎАВХХAЃЌBСНжжаЭКХЕФЛњЦїЙВ10ЬЈвЛЦ№МгЙЄвЛХњИУСуМўЃЌЮЊСЫШчЦкЭъГЩШЮЮёЃЌвЊЧѓСНжжЛњЦїУПаЁЪБМгЙЄЕФСуМўВЛЩйгк72МўЃЌЭЌЪБЮЊСЫБЃеЯЛњЦїЕФе§ГЃдЫзЊЃЌСНжжЛњЦїУПаЁЪБМгЙЄЕФСуМўВЛФмГЌЙ§76МўЃЌФЧУДAЃЌBСНжжаЭКХЕФЛњЦїПЩвдИїАВХХЖрЩйЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
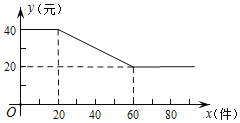
ЁОЬтФПЁПвЛжжЛ№БЌЕФЭјКьЕчзгВњЦЗЃЌУПМўВњЦЗГЩБО![]() дЊЁЂЙЄГЇНЋИУВњЦЗНјааЭјТчХњЗЂЃЌХњЗЂЕЅМл
дЊЁЂЙЄГЇНЋИУВњЦЗНјааЭјТчХњЗЂЃЌХњЗЂЕЅМл![]() ЃЈдЊЃЉгывЛДЮадХњЗЂСП
ЃЈдЊЃЉгывЛДЮадХњЗЂСП![]() ЃЈМўЃЉЃЈ
ЃЈМўЃЉЃЈ![]() ЮЊе§ећЪ§ЃЉжЎМфТњзуШчЭМЫљЪОЕФКЏЪ§ЙиЯЕЃЎ
ЮЊе§ећЪ§ЃЉжЎМфТњзуШчЭМЫљЪОЕФКЏЪ§ЙиЯЕЃЎ
![]() жБНгаДГі
жБНгаДГі![]() гы
гы![]() жЎМфЫљТњзуЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП
жЎМфЫљТњзуЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
![]() ШєвЛДЮадХњЗЂСПВЛГЌЙ§
ШєвЛДЮадХњЗЂСПВЛГЌЙ§![]() МўЃЌЕБХњЗЂСПЮЊЖрЩйМўЪБЃЌЙЄГЇЛёРћзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
МўЃЌЕБХњЗЂСПЮЊЖрЩйМўЪБЃЌЙЄГЇЛёРћзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
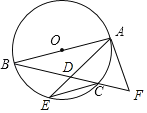
ЁОЬтФПЁПШчЭМЃЌ![]() ФкНггкЁб
ФкНггкЁб![]() ЃЌ
ЃЌ![]() ЪЧЁб
ЪЧЁб![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() жС
жС![]() ЕуЃЌЪЙ
ЕуЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХаЖЯжБЯп![]() гыЁб
гыЁб![]() ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФБпаЮ![]() ЪЧ
ЪЧ![]() ЕФдВФкНгЫФБпаЮЃЌЯпЖЮ
ЕФдВФкНгЫФБпаЮЃЌЯпЖЮ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌСЌНс
ЕФжБОЖЃЌСЌНс![]() ЃЎЕу
ЃЎЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛЕуЃЌСЌНс
ЩЯЕФвЛЕуЃЌСЌНс![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпгы
ЕФбгГЄЯпгы![]() ЕФбгГЄЯпЯрНЛгыЕу
ЕФбгГЄЯпЯрНЛгыЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]()
ЂйЧѓжЄЃК![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЛ
ЮЊЕШбќжБНЧШ§НЧаЮЃЛ
ЂкЧѓ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
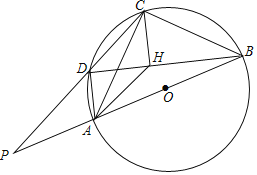
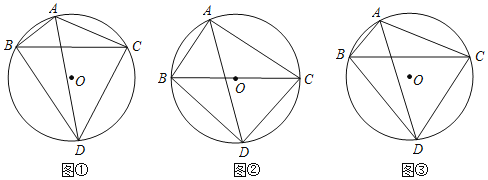
ЁОЬтФПЁПвбжЊ![]() ABCФкНггк
ABCФкНггк![]() ЃЌ
ЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕуDЃЌСЌНгDBЃЌDCЃЎ
гкЕуDЃЌСЌНгDBЃЌDCЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБ![]() ЪБЃЌЧыжБНгаДГіЯпЖЮABЃЌACЃЌADжЎМфТњзуЕФЕШСПЙиЯЕЪНЃКЁЁ ЁЁЃЛ
ЪБЃЌЧыжБНгаДГіЯпЖЮABЃЌACЃЌADжЎМфТњзуЕФЕШСПЙиЯЕЪНЃКЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕБ![]() ЪБЃЌЪдЬНОПЯпЖЮABЃЌACЃЌADжЎМфТњзуЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЪБЃЌЪдЬНОПЯпЖЮABЃЌACЃЌADжЎМфТњзуЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌШєBC=5ЃЌBD=4ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЬсИпХЉЬяРћгУаЇвцЃЌФГЕигЩУПФъжжжВЫЋМОЕОИФЮЊЯШбјжГаЁСњЯКдйжжжВвЛМОЫЎЕОЕФЁАЯКЕОЁБТжзїФЃЪНЃЎФГХЉЛЇгаХЉЬя20ФЖЃЌШЅФъПЊЪМЪЕЪЉЁАЯКЕОЁБТжзїЃЌШЅФъГіЪлаЁСњЯКУПЧЇПЫЛёЕУЕФРћШѓЮЊ32дЊ(РћШѓЃНЪлМлЉГЩБО)ЃЎгЩгкПЊЗЂГЩБОЯТНЕКЭЪаГЁЙЉЧѓЙиЯЕБфЛЏЃЌНёФъУПЧЇПЫаЁСњЯКЕФбјжГГЩБОЯТНЕ25%ЃЌЪлМлЯТНЕ10%ЃЌГіЪлаЁСњЯКУПЧЇПЫЛёЕУРћШѓЮЊ30дЊЃЎ
(1)ЧѓШЅФъУПЧЇПЫаЁСњЯКЕФбјжГГЩБОгыЪлМлЃЛ
(2)ИУХЉЛЇНёФъУПФЖХЉЬяЪеЛёаЁСњЯК100ЧЇПЫЃЌШєНёФъЕФЫЎЕОжжжВГЩБОЮЊ600дЊ/ФЖЃЌЕОЙШЪлМлЮЊ25дЊ/ЧЇПЫЃЌИУХЉЛЇЙРМЦНёФъПЩЛёЕУЁАЯКЕОЁБТжзїЪеШыВЛЩйгк8ЭђдЊЃЌдђЕОЙШЕФФЖВњСПжСЩйЛсДяЕНЖрЩйЧЇПЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
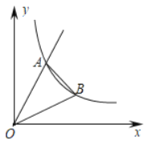
ЁОЬтФПЁПШчЭМЃЌе§БШР§КЏЪ§y1ЃНk1xЕФЭМЯѓгыЗДБШР§КЏЪ§y2ЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЯрНЛгкЕуAЃЈ
ЃЈxЃО0ЃЉЕФЭМЯѓЯрНЛгкЕуAЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЃЌЕуBЪЧЗДБШР§КЏЪ§ЭМЯѓЩЯвЛЕуЃЌЫќЕФКсзјБъЪЧ3ЃЌСЌНгOBЃЌABЃЌдђЁїAOBЕФУцЛ§ЪЧ_____ЃЎ
ЃЉЃЌЕуBЪЧЗДБШР§КЏЪ§ЭМЯѓЩЯвЛЕуЃЌЫќЕФКсзјБъЪЧ3ЃЌСЌНгOBЃЌABЃЌдђЁїAOBЕФУцЛ§ЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com