
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
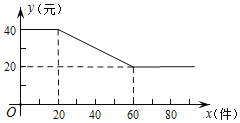
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?
科目:初中数学 来源: 题型:
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了抓住夏季来临,衬衫热销的契机,决定用46000元购进![]() 、
、![]() 、
、![]() 三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件.设购进
三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件.设购进![]() 种型号的衬衣
种型号的衬衣![]() 件,购进
件,购进![]() 种型号的衬衣
种型号的衬衣![]() 件,三种品牌的衬衫的进价和售价如下表所示:
件,三种品牌的衬衫的进价和售价如下表所示:
型号 |
|
|
|
进价(元/件) | 100 | 200 | 150 |
售价(元/件) | 200 | 350 | 300 |
(Ⅰ)直接用含![]() 、
、![]() 的代数式表示购进
的代数式表示购进![]() 种型号衬衣的件数,其结果可表示为______;
种型号衬衣的件数,其结果可表示为______;
(Ⅱ)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅲ)如果该商场能够将购进的衬衫全部售出,但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元.
①求利润![]() (元)与
(元)与![]() (件)之间的函数关系式;
(件)之间的函数关系式;
②求商场能够获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
(1)分别求出选择这两种卡消费时,y关于x的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
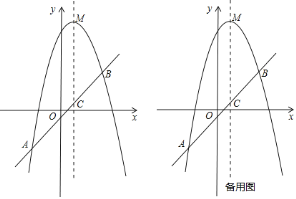
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ),
),![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
(4)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
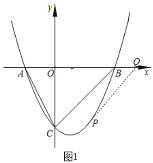
【题目】如图1,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,线段
的坐标为__________,线段![]() 的长为__________,抛物线的解析式为__________.
的长为__________,抛物线的解析式为__________.
(2)点![]() 是线段
是线段![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
①如果在![]() 轴上存在点
轴上存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.求点
为顶点的四边形是平行四边形.求点![]() 的坐标.
的坐标.
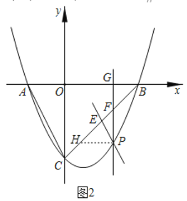
②如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,记
,记![]() ,求
,求![]() 关于
关于![]() 的函数解析式;当
的函数解析式;当![]() 取
取![]() 和
和![]() 时,试比较
时,试比较![]() 的对应函数值
的对应函数值![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
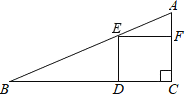
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com