
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() 两点,与y轴交于点C,
两点,与y轴交于点C,![]() .
.
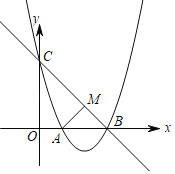
(1)求抛物线的解析式及顶点D的坐标;
(2)过点A作![]() ,垂足为M,求证:四边形ADBM为正方形;
,垂足为M,求证:四边形ADBM为正方形;
(3)点P为抛物线在直线BC下方图形上的一动点,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(4)若点Q为线段OC上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
【答案】(1)抛物线的表达式为:![]() ,顶点
,顶点![]() ;(2)证明见解析;(3)点
;(2)证明见解析;(3)点![]() ;(4)存在,
;(4)存在,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)设交点式![]() ,利用待定系数法进行求解即可;
,利用待定系数法进行求解即可;
(2)先证明四边形ADBM为菱形,再根据有一个角是直角的菱形是正方形即可得证;
(3)先求出直线BC的解析式,过点P作y轴的平行线交BC于点N,设点![]() ,则点N
,则点N![]() ,根据
,根据![]() 可得关于x的二次函数,继而根据二次函数的性质进行求解即可;
可得关于x的二次函数,继而根据二次函数的性质进行求解即可;
(4)存在,如图,过点C作与y轴夹角为![]() 的直线CF交x轴于点F,过点A作
的直线CF交x轴于点F,过点A作![]() ,垂足为H,交y轴于点Q, 此时
,垂足为H,交y轴于点Q, 此时![]() ,则
,则![]() 最小值
最小值![]() ,求出直线HC、AH的解析式即可求得H点坐标,进行求得AH的长即可得答案.
,求出直线HC、AH的解析式即可求得H点坐标,进行求得AH的长即可得答案.
(1)函数的表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
则顶点![]() ;
;
(2)![]() ,
,![]() ,
,
∵A(1,0),B(3,0),∴ OB=3,OA=1,
∴AB=2,
∴![]() ,
,
又∵D(2,-1),
∴AD=BD=![]() ,
,
∴AM=MB=AD=BD,
∴四边形ADBM为菱形,
又∵![]() ,
,
![]() 菱形ADBM为正方形;
菱形ADBM为正方形;
(3)设直线BC的解析式为y=mx+n,
将点B、C的坐标代入得:![]() ,
,
解得:![]() ,
,
所以直线BC的表达式为:y=-x+3,
过点P作y轴的平行线交BC于点N,
设点![]() ,则点N
,则点N![]() ,
,
则![]() ,
,
![]() ,故
,故![]() 有最大值,此时
有最大值,此时![]() ,
,
故点![]() ;
;
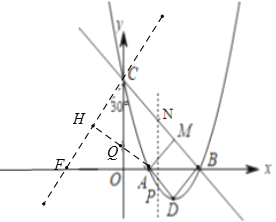
(4)存在,理由:
如图,过点C作与y轴夹角为![]() 的直线CF交x轴于点F,过点A作
的直线CF交x轴于点F,过点A作![]() ,垂足为H,交y轴于点Q,
,垂足为H,交y轴于点Q,
此时![]() ,
,
则![]() 最小值
最小值![]() ,
,
在Rt△COF中,∠COF=90°,∠FOC=30°,OC=3,tan∠FCO=![]() ,
,
∴OF=![]() ,
,
∴F(-![]() ,0),
,0),
利用待定系数法可求得直线HC的表达式为:![]() …①,
…①,
∵∠COF=90°,∠FOC=30°,
∴∠CFO=90°-30°=60°,
∵∠AHF=90°,
∴∠FAH=90°-60°=30°,
∴OQ=AOtan∠FAQ=![]() ,
,
∴Q(0,![]() ),
),
利用待定系数法可求得直线AH的表达式为:![]() …②,
…②,
联立①②并解得:![]() ,
,
故点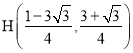 ,而点
,而点![]() ,
,
则![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.


科目:初中数学 来源: 题型:
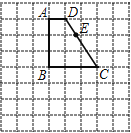
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形![]() 的顶点在格点上,点
的顶点在格点上,点![]() 是边
是边![]() 与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由
与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由
(1)如图1,过点![]() 画线段
画线段![]() ,使
,使![]() ,且
,且![]()
(2)如图1,在边![]() 上画一点
上画一点![]() ,使
,使![]()
(3)如图2,过点![]() 画线段
画线段![]() ,使
,使![]() ,且
,且![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
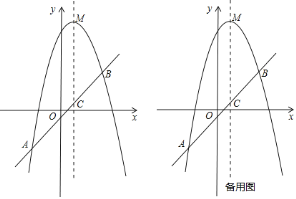
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
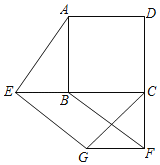
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作FG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
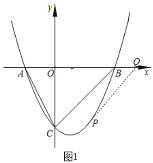
【题目】如图1,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,线段
的坐标为__________,线段![]() 的长为__________,抛物线的解析式为__________.
的长为__________,抛物线的解析式为__________.
(2)点![]() 是线段
是线段![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
①如果在![]() 轴上存在点
轴上存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.求点
为顶点的四边形是平行四边形.求点![]() 的坐标.
的坐标.
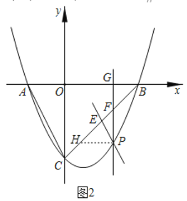
②如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,记
,记![]() ,求
,求![]() 关于
关于![]() 的函数解析式;当
的函数解析式;当![]() 取
取![]() 和
和![]() 时,试比较
时,试比较![]() 的对应函数值
的对应函数值![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为A、B、C、D、E,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 | 频率 |
A | m |
B | 0.35 |
C | 0.20 |
D | n |
E | 0.05 |
(1)求本次调查的小型汽车数量及m,n的值;
(2)补全频数分布直方图;
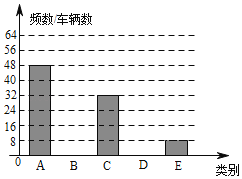
(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
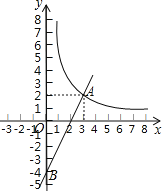
(1)求函数![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)结合图象直接写出不等式组0<![]() <kx+b的解集.
<kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
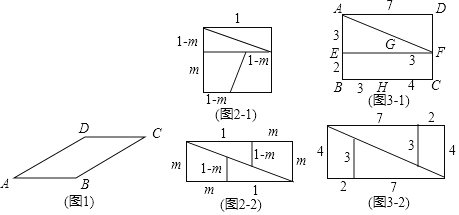
【题目】(1)如图1,在平行四边形ABCD中,∠A=30°,AB=6,AD=8,将平行四边形ABCD分割成两部分,然后拼成一个矩形,请画出拼成的矩形,并说明矩形的长和宽.(保留分割线的痕迹)
(2)若将一边长为1的正方形按如图2﹣1所示剪开,恰好能拼成如图2﹣2所示的矩形,则m的值是多少?
(3)四边形ABCD是一个长为7,宽为5的矩形(面积为35),若把它按如图3﹣1所示的方式剪开,分成四部分,重新拼成如图3﹣2所示的图形,得到一个长为9,宽为4的矩形(面积为36).问:重新拼成的图形的面积为什么会增加?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上学习越来越受到学生的喜爱.某校信息小组为了解七年级学生网上学习的情况,从该校七年级随机抽取20名学生,进行了每周网上学习的调查.数据如下(单位:时):
3 | 2.5 | 0.6 | 1.5 | 1 | 2 | 2 | 3.3 | 2.5 | 1.8 |
2.5 | 2.2 | 3.5 | 4 | 1.5 | 2.5 | 3.1 | 2.8 | 3.3 | 2.4 |
整理上面的数据,得到表格如下:
网上学习时间 |
|
|
|
|
人数 | 2 | 5 | 8 | 5 |
样本数据的平均数、中位数、众数如下表所示:
统计量 | 平均数 | 中位数 | 众数 |
数值 | 2.4 |
|
|
根据以上信息,解答下列问题:
(1)上表中的中位数![]() 的值为 ,众数
的值为 ,众数![]() 的值为 .
的值为 .
(2)用样本中的平均数估计该校七年级学生平均每人一学期(按18周计算)网上学习的时间.
(3)已知该校七年级学生有200名,估计每周网上学习时间超过2小时的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com