
【题目】如图1,![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,且
,且![]() ,点
,点![]() 在
在 ![]() 上,连接
上,连接![]() .
.
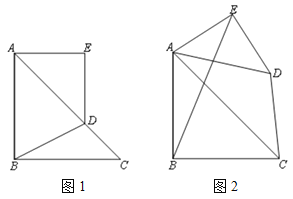
(1)如果![]() ,①求
,①求![]() ;②若
;②若![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实数根,求
的两个实数根,求![]() 的值;
的值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,连接
,连接![]() ,求五边形
,求五边形![]() 的面积.
的面积.
【答案】(1)①![]() ,②
,②![]() ;(2)五边形
;(2)五边形![]() 的面积为
的面积为![]() .
.
【解析】
(1)①延长ED交BC于点F,表示出DF、BF,然后利用勾股定理列出方程,再把c=![]() a代入求出a、b的关系即可;
a代入求出a、b的关系即可;
②利用根与系数的关系表示出a+b,ab,然后消掉a、b得到关于m的一元二次方程,然后求解即可;
(2)过A,C,D分别向BE作垂线,垂足分别为H,M,N,根据同角的余角相等求出∠HAE=∠NED,然后利用“角角边”证明△AHE和△END全等,同理可证△AHB≌BMC,根据全等三角形对应边相等可得AH=MB=EN,MC=BH,DN=EH,设AH=h,然后根据五边形的面积等于两对全等三角形的面积加上梯形的面积列式整理即可得解.
(1)①延长ED交BC于点F,
![]() ,
,
在![]() 中由勾股定理得,
中由勾股定理得, ![]() ,
,
又![]()
![]() ,
,
![]() 或
或![]() ,
,
又![]() ,
,
∴![]() ;
;
②由根与系数的关系![]() ,
,
由![]() ,
,
解得![]() ,
,
所以, ![]() ,
,
整理得, ![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,方程为
时,方程为![]() ,这个方程有两个不相等的正根,
,这个方程有两个不相等的正根,
所以,![]() 符合题意;
符合题意;
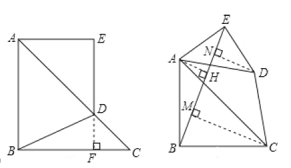
(2)过![]() 分别向
分别向![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
![]() ,
,
![]()
同理可证![]() ,
,
则![]() ,
,
设![]() ,
,
五边形![]() 的面积为
的面积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一张长方形纸片,AB=CD=a,AD=BC=b(a<b<2a).
将这张纸片沿着过点A的折痕翻折,使点B落在AD边上的点F,折痕交BC于点E,将折叠后的纸片再次沿着另一条过点A的折痕翻折,点E恰好与点D重合,此时折痕交DC于点G.
(1)在图中确定点F、点E和点G的位置;
(2)连接AE,则∠EAB= °;
(3)用含有a、b的代数式表示线段DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
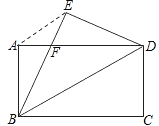
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)AE∥BD;
(3)若AB=6,AD=8,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
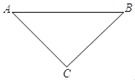
【题目】如图,在Rt△ABC中,AC=BC,AB=10,以AB为斜边向上作Rt△ABD,使∠ADB=90°.连接CD,若CD=7![]() ,则AD=_____.
,则AD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )
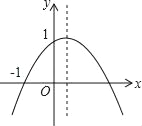
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
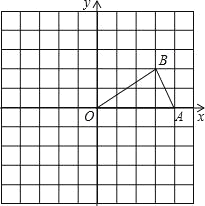
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
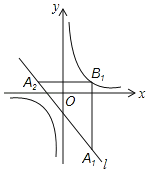
【题目】如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=![]() ,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三一班五个劳动竞赛小组一天植树的棵数是:10,10,12,x,8,如果这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 12 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com