
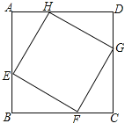
【题目】已知:正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,且AE=BF=CG=DH,
(1)四边形EFGH是正方形吗?为什么?
(2)若正方形ABCD的边长为4cm,且AE=BF=CG=DH=3cm,请求出四边形EFGH的面积.
【答案】(1)是正方形,理由见解析;(2)10.
【解析】
(1)由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGF是菱形,再证出∠HEF=90°,即可得出结论;
(2)根据勾股定理求得正方形的边长,然后即可求得面积.
解:(1)四边形EFGH是正方形;
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA
∵AE=BF=CG=DH
∴AH=BE=CF=DG
在△AEH、△BFE、△CGF和△DHG中
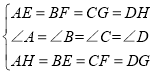
∴△AEH≌△BFE≌△CGF≌△DHG(SAS)
∴EH=FE=GF=GH,∠AEH=∠BFE
∴四边形EFGH是菱形
∵∠BEF+∠BFE=90°
∴∠BEF+∠AEH=90°
∴∠HEF=90°
∴四边形EFGH是正方形;
(2)∵正方形ABCD的边长为4cm,且AE=BF=CG=DH=1cm,
∴AE=BF=CG=DH=3
∴正方形EFGH的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE=BF.求证:
(1)AE=CF;
(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为非负整数,且该方程的根都是无理数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
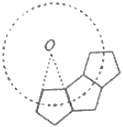
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
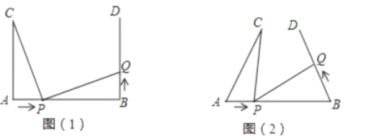
【题目】如图(1),![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动,它们运动的时间为
运动,它们运动的时间为![]()
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,判断线段
时,判断线段![]() 与
与![]() 满足的关系,并说明理由;
满足的关系,并说明理由;
(2)如图(2),将图(1)中的“![]() ,
,![]() ”为改“
”为改“![]() ”,其它条件不变.设点
”,其它条件不变.设点![]() 的运动速度为
的运动速度为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 全等?若存在,求出相应的
全等?若存在,求出相应的![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2011次运动后,动点P的坐标是( )
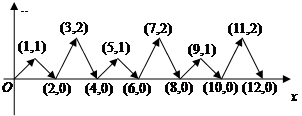
A.(2011,0)B.(2011,1)C.(2011,2)D.(2010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项ax2+bx+c式的配方法.
例如:x2+11x+24=x2+11x+![]()
![]() +24=
+24=![]()
![]()
探究发现:
小明发现:
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如: x2+11x+24=x2+11x+![]()
![]() +24=
+24=![]()
![]() =
=![]()
![]() =(x+8)(x+3)
=(x+8)(x+3)
小红发现:运用多项式的配方法能确定一些多项式的最大值或最小值.
x2+11x+24=x2+11x+![]()
![]() +24=
+24=![]()
![]()
因为不论x取何值,![]() ,所以当
,所以当![]() ,时,多项式x2+11x+24有最小值为
,时,多项式x2+11x+24有最小值为![]()
根据以上材料,解答下列问题:
(1)分解因式:x23x10;
(2)试确定:多项式![]() 的最值(即最大值或最小值).
的最值(即最大值或最小值).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com