
分析 首先根据关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2-(a2+1)x-2a+1的图象不经过点(-1,6)确定a的值,然后利用概率公式求解.
解答 解:∵使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,
∴[-2(a-1)]2-4×1×a(a-3)>0,
解得:a>-1,
∵以x为自变量的二次函数y=x2-(a2+1)x-2a+1的图象不经过点(-1,6),
∴12+(a2+1)-2a+1≠6,
∴a≠-1且a≠3,
∴满足条件的a只有0和1和2,
∴则使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2-(a2+1)x-2a+1的图象不经过点(-1,6)的概率是$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间的连线中,直线最短 | |
| B. | 两点一定能确定一条直线 | |
| C. | 若AP=BP,则P是线段AB的中点 | |
| D. | 两点之间的线段叫做这两点之间的距离 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
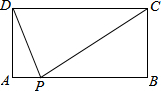 如图,矩形ABCD中,AB=5,AD=2,点P是AB边上不与A、B重合的点,要使△DPA与△PCB相似(相似比不为1),需加一个条件,这个条件是∠DPC=90°.
如图,矩形ABCD中,AB=5,AD=2,点P是AB边上不与A、B重合的点,要使△DPA与△PCB相似(相似比不为1),需加一个条件,这个条件是∠DPC=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com