
【题目】阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
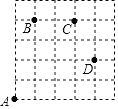
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中B→C( , )C→D( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程S.
【答案】(1)+2,0,+1,﹣2;(2)若甲虫从A到P的行走路线依次为:A→E→F→P,图中P的即为所求.见解析;(3)甲虫走过的总路程为16.
【解析】
(1)B→C只向右走3格;C→D先向右走1格,再向下走2格,由此写出即可.
(2)由(+3,+2)→(+1,+3)→(+1,﹣2)可知从A处右移3格,上移2格,再右移1格,上移3格,右移1格,下移2格即是甲虫P处的位置;
(3)由A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2)知:先向右移动1格,向上移动4格,向右移动2格,再向右移动1格,向下移动2格,最后向左移动4格,向下移动2格,把移动的距离相加即可.
(1)图中B→C(+2.0),C→D(+1,﹣2).
故答案为:+2,0,+1,﹣2.
(2)若甲虫从A到P的行走路线依次为:A→E→F→P,图中P的即为所求.
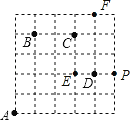
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),
甲虫走过的总路程S=1+4+2+1+2+4+2=16.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;
②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.
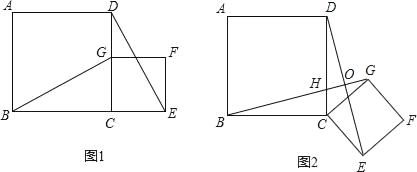
(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.
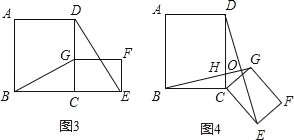
(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=![]() ,求BE2+DG2的值.
,求BE2+DG2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
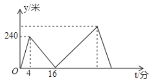
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )
(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班各选派10名学生参加“垃圾分类知识竞赛,各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 |
| 93 | 93 | 12 |
八(2)班 | 99 | 95 |
|
| 8.4 |
(1)求表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)依据数据分析表,有同学认为最高分在(1)班,(1)班的成绩比(2)班好.但也有同学认为(2)班的成绩更好.请你写出两条支持八(2)班成绩更好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的![]() ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
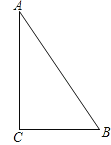
【题目】如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点 C. AC中点 D.∠C的平分线与AB的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料:如图(1),在数轴上![]() 示的数为
示的数为![]() ,
,![]() 点表示的数为
点表示的数为![]() ,则点
,则点![]() 到点
到点![]() 的距离记为
的距离记为![]() .线段
.线段![]() 的长可以用右边的数减去左边的数表示,即
的长可以用右边的数减去左边的数表示,即![]() .
.
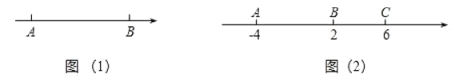
解决问题:如图(2),数轴上点![]() 表示的数是-4,点
表示的数是-4,点![]() 表示的数是2,点
表示的数是2,点![]() 表示的数是6.
表示的数是6.
(1)若数轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 表示的数为 ;
表示的数为 ;
(2)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,若点
以每秒1个单位长度的速度向左运动,同时,若点![]() 和点
和点![]() 分别以每秒2个单位长度和3个单位长度的速度向右运动,假设
分别以每秒2个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .则点
.则点![]() 表示的数是 (用含
表示的数是 (用含![]() 的代数式表示),
的代数式表示),![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(3)请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com