
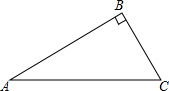
 已知,如图Rt△ABC中,AB=8,BC=6,求sin∠A和tan∠A.
已知,如图Rt△ABC中,AB=8,BC=6,求sin∠A和tan∠A.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
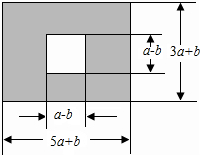 如图,某市有长为(5a+b)米,宽为(3a+b)米的长方形地块,计划将阴影部分用每块面积为2a平方米的草坪进行绿化,中间将修建一座雕像,则绿化至少需要这样的草坪多少块?并求出当a=3,b=-1时的值.
如图,某市有长为(5a+b)米,宽为(3a+b)米的长方形地块,计划将阴影部分用每块面积为2a平方米的草坪进行绿化,中间将修建一座雕像,则绿化至少需要这样的草坪多少块?并求出当a=3,b=-1时的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一只小蝴蝶在空中自由自在飞行,然后它随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小蝴蝶停在黑色方格中的概率是( )
一只小蝴蝶在空中自由自在飞行,然后它随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小蝴蝶停在黑色方格中的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
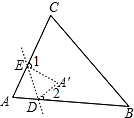 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )
如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=65°,则∠1+∠2=( )| A. | 210° | B. | 130° | C. | 115° | D. | 65° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com