
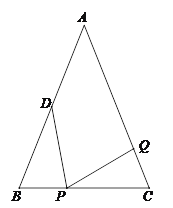
【题目】如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为______cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?
【答案】(1)1s;(2)①点Q的运动速度为![]() cm/s时,能使△BPD≌△CPQ;②点P、Q在AC边上相遇,相遇地点距离C点4cm处.
cm/s时,能使△BPD≌△CPQ;②点P、Q在AC边上相遇,相遇地点距离C点4cm处.
【解析】
(1)①根据时间和速度分别求得两个三角形中的边的长,根据![]() 判定两个三角形全等.
判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点![]() 运动的时间,再求得点
运动的时间,再求得点![]() 的运动速度;
的运动速度;
(2)根据题意结合图形分析发现:由于点![]() 的速度快,且在点
的速度快,且在点![]() 的前边,所以要想第一次相遇,则应该比点
的前边,所以要想第一次相遇,则应该比点![]() 多走等腰三角形的两个边长.
多走等腰三角形的两个边长.
(1)①全等.理由如下:
证明:∵t=1秒,
∴BP=CQ=1×1=1 cm,
∵AB=6cm,
点D为AB的中点,
∴BD=3cm.
又∵PC=BC﹣BP,BC=4cm,
∴PC=4-1=3cm,
∴PC=BD.
又∵AB=AC,∴∠B=∠C,
![]()
②假设![]()
![]()
又![]()
则![]()
∴点P,点Q运动的时间![]() 秒,
秒,
![]()
(2)设经过x秒后点P与点Q第一次相遇,
由题意得:1.5x=x+2×6,解得x=24.
∴点P共运动了24×1m/s=24cm.
∵24=16+4+4 ∴点P、点Q在AC边上相遇,
∴经过24秒点P与点Q第一次在边AC上相遇.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
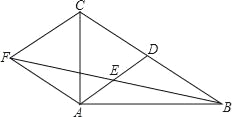
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)试判断四边形ADCF的形状,并证明;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
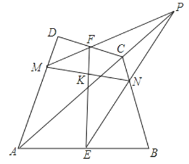
【题目】如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.
求证:K是线段MN的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
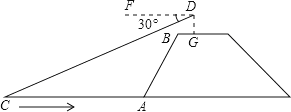
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
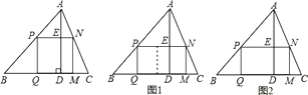
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2![]() ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在 ![]() 上的点D处,折痕交OA于点C,则阴影部分的面积是________.
上的点D处,折痕交OA于点C,则阴影部分的面积是________.
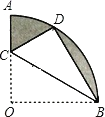
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一种游戏:三张大小,质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,如果和为奇数,则小明胜,若和为偶数则小亮胜.
(1)用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况.
(2)请判断该游戏对双方是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:∠1=∠2;
②如图2,若BF=2AF,连接CF,求证:BF⊥CF;
(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求![]() 的值.
的值.
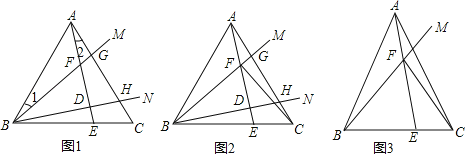
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com