
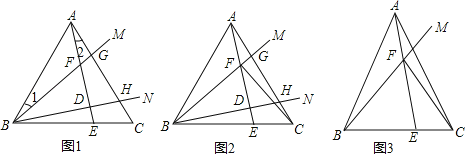
【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:∠1=∠2;
②如图2,若BF=2AF,连接CF,求证:BF⊥CF;
(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求![]() 的值.
的值.
【答案】(1)①见解析;②见解析;(2)2
【解析】
(1)①只要证明∠2+∠BAF=∠1+∠BAF=60°即可解决问题;
②只要证明△BFC≌△ADB,即可推出∠BFC=∠ADB=90°;
(2)在BF上截取BK=AF,连接AK.只要证明△ABK≌CAF,可得S△ABK=S△AFC,再证明AF=FK=BK,可得S△ABK=S△AFK,即可解决问题;
(1)①证明:如图1中,
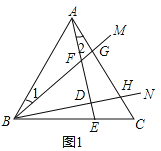
∵AB=AC,∠ABC=60°
∴△ABC是等边三角形,
∴∠BAC=60°,
∵AD⊥BN,
∴∠ADB=90°,
∵∠MBN=30°,
∠BFD=60°=∠1+∠BAF=∠2+∠BAF,
∴∠1=∠2
②证明:如图2中,
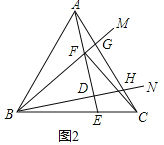
在Rt△BFD中,∵∠FBD=30°,
∴BF=2DF,
∵BF=2AF,
∴BF=AD,
∵∠BAE=∠FBC,AB=BC,
∴△BFC≌△ADB,
∴∠BFC=∠ADB=90°,
∴BF⊥CF
(2)在BF上截取BK=AF,连接AK.

∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,
∴∠CFB=∠2+∠4+∠BAC,
∵∠BFE=∠BAC=2∠EFC,
∴∠1+∠4=∠2+∠4
∴∠1=∠2,∵AB=AC,
∴△ABK≌CAF,
∴∠3=∠4,S△ABK=S△AFC,
∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,
∴∠KAF=∠1+∠3=∠AKF,
∴AF=FK=BK,
∴S△ABK=S△AFK,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
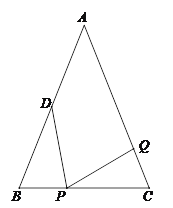
【题目】如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为______cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+8分别交x轴,y轴于点A,B,直线y![]() x+3交y轴于点C,两直线相交于点D.
x+3交y轴于点C,两直线相交于点D.

(1)求点D的坐标;
(2)如图2,过点A作AE∥y轴交直线y![]() x+3于点E,连接AC,BE.求证:四边形ACBE是菱形;
x+3于点E,连接AC,BE.求证:四边形ACBE是菱形;
(3)如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG,FG,当CG=FG,且∠CGF=∠ABC时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),点
重合),点![]() 为线段
为线段![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]() .
.
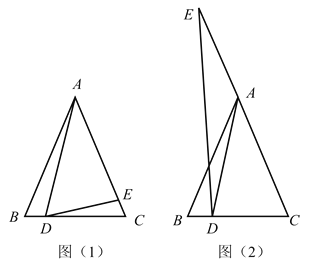
(1)如图(1),
①若![]() ,
,![]() ,则
,则![]() ____________,
____________,![]() _______________.
_______________.
②若![]() ,
,![]() ,则
,则![]() ____________,
____________,![]() ______________.
______________.
③写出![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)如图(2),当![]() 点在
点在![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
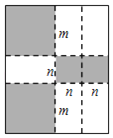
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 ;
(2)若每块小矩形的面积为10cm2,两个大正方形和两个小正方形的面积和为58cm2,试求m+n的值
(3)②图中所有裁剪线(虚线部分)长之和为 cm.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为![]() 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产![]() 件,每件利润
件,每件利润![]() 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加![]() 元.
元.
(1)每件利润为![]() 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少![]() 件.若生产第
件.若生产第![]() 档的产品一天的总利润为
档的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ≤
≤![]() ≤
≤![]() ),求出
),求出![]() 关于
关于![]() 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为![]() 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东台市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知![]() 年投资
年投资![]() 万元,预计
万元,预计![]() 年投资
年投资![]() 万元.若这两年内平均每年投资增长的百分率相同.
万元.若这两年内平均每年投资增长的百分率相同.
![]() 求平均每年投资增长的百分率;
求平均每年投资增长的百分率;
![]() 按此增长率,计算
按此增长率,计算![]() 年投资额能否达到
年投资额能否达到![]() 万?
万?
查看答案和解析>>
科目:初中数学 来源: 题型:
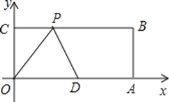
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 、
、![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上运动,当
边上运动,当![]() 是以腰长为5的等腰三角形时,点
是以腰长为5的等腰三角形时,点![]() 的坐标为________________.
的坐标为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com