【题目】折叠长方形
的一边
，使点
落在边
的点
处，若
，求
的长为（ ）
A.
B.
C.
D.
【答案】A
【解析】
在Rt△ABF中，根据勾股定理求出BF的值，进而得出FC=BC-BF=10-6=4cm．在Rt△EFC中，根据勾股定理即可求出EC的长.
设EC的长为xcm，
∴DE=（8-x）cm．
∵△ADE折叠后的图形是△AFE，
∴AD=AF，∠D=∠AFE，DE=EF．
∵AD=BC=10cm，
∴AF=AD=10cm．
又∵AB=8cm，在Rt△ABF中，根据勾股定理，得AB2+BF2=AF2，
∴82+BF2=102，
∴BF=6cm．
∴FC=BC-BF=10-6=4cm．
在Rt△EFC中，根据勾股定理，得：FC2+EC2=EF2，
∴42+x2=（8-x）2，即16+x2=64-16x+x2，
化简，得16x=48．
∴x=3．
故EC的长为3cm．
故答案为：A．
天天向上口算本系列答案科目：初中数学 来源： 题型：
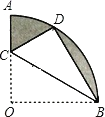
【题目】如图，在扇形OAB中，∠AOB=90°，半径OA=2
，将扇形OAB沿过点B的直线折叠，点O恰好落在 
上的点D处，折痕交OA于点C，则阴影部分的面积是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,四边形ABCD中，∠B=90°, AB//CD，M为BC边上的一点，AM平分∠BAD，DM平分∠ADC，
求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目：初中数学 来源： 题型：
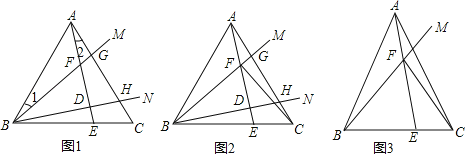
【题目】已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．
（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．
①求证：∠1＝∠2；
②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；
（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某数学活动小组在作等边三角形的拓展图形，研究其性质时，经历了如下过程：
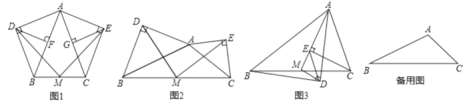
操作发现：在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是____(填序号即可)
；
；
整个图形是轴对称图形；
．
数学思考：在任意
中，分别以AB和AC为斜边，向的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD与ME具有怎样的数量和位置关系？请给出证明过程；
类比研究：在任意中，仍分别以AB和AC为斜边，向的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断
的形状？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列格式， 
- 
， 
， 
， 
…
（1）化简以上各式，并计算出结果；
（2）以上格式的结果存在一定的规律，请按规律写出第5个式子及结果.
（3）用含n（n≥1的整数）的式子写出第n个式子及结果，并给出证明的过程.
查看答案和解析>>
科目：初中数学 来源： 题型：
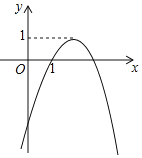
【题目】如图，二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，①abc＜0，②2a+b＞0，③a-b+c＜0，④b2＞4ac，⑤关于x的方程ax2+bx+c-2=0没有实数根．则下列结论正确的有______．（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】□ABCD中，E、F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（ ）
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
