
【题目】已知二次函数![]() 的图象如图所示,下列结论:①
的图象如图所示,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 与
与![]() 都是负数,其中结论正确的序号是________.
都是负数,其中结论正确的序号是________.
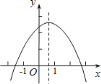
【答案】②③
【解析】
根据函数的开口方向,对称轴以及与y轴的交点即可确定a,b,c的符号,从而判断①;根据对称轴的位置即可判断②;根据二次函数与x轴的交点的坐标,即可确定![]() 的范围,确定
的范围,确定![]() 与-1的大小,从而判断a+c的符号;根据x=2和-2时,点的坐标的符号判断④.
与-1的大小,从而判断a+c的符号;根据x=2和-2时,点的坐标的符号判断④.
解:∵函数的开口向下,
∴a<0,
∵函数与y轴的正半轴相交,
∴c>0,
∵对称轴x=-![]() >0,
>0,
∴b>0,
∴abc<0,
故①错误、②正确.
二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点的横坐标异号,因而方程ax2+bx+c=0又两个异号的根,且方程的两个x1,x2,不妨设x1<x2,则-2<x1<-1,且2<x2<3.则-6<![]() <-3<-1.
<-3<-1.
∴a+c>0,故③正确;
当x=-2时,函数的纵坐标小于0,即y=4a-2b+c<0,
当x=2时,函数的纵坐标大于0,则y=4a+2b+c>0,
故④错误.
故正确的是:②③.
故答案是:②③.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
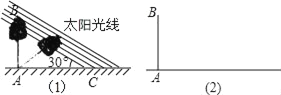
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),点
重合),点![]() 为线段
为线段![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]() .
.
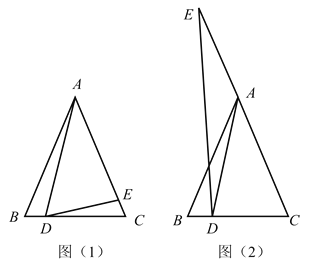
(1)如图(1),
①若![]() ,
,![]() ,则
,则![]() ____________,
____________,![]() _______________.
_______________.
②若![]() ,
,![]() ,则
,则![]() ____________,
____________,![]() ______________.
______________.
③写出![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)如图(2),当![]() 点在
点在![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为![]() 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产![]() 件,每件利润
件,每件利润![]() 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加![]() 元.
元.
(1)每件利润为![]() 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少![]() 件.若生产第
件.若生产第![]() 档的产品一天的总利润为
档的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ≤
≤![]() ≤
≤![]() ),求出
),求出![]() 关于
关于![]() 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为![]() 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:(1)求出y与x之间的函数关系式;(2)如果商店销售这种商品,每天要获得1500元利润,那么每件商品的销售价应定为多少元?(3)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
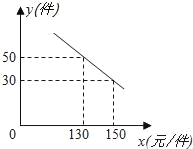
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东台市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知![]() 年投资
年投资![]() 万元,预计
万元,预计![]() 年投资
年投资![]() 万元.若这两年内平均每年投资增长的百分率相同.
万元.若这两年内平均每年投资增长的百分率相同.
![]() 求平均每年投资增长的百分率;
求平均每年投资增长的百分率;
![]() 按此增长率,计算
按此增长率,计算![]() 年投资额能否达到
年投资额能否达到![]() 万?
万?
查看答案和解析>>
科目:初中数学 来源: 题型:
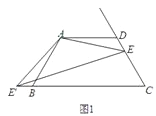
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
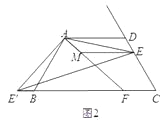
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
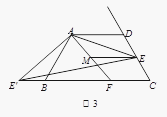
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com