
����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
����������ŷ��(Leonhard Euler)����ʿ��ѧ�ң�����ѧ�Ͼ�������������������������Ҫ��������ʽ�Ͷ�����������ŷ�����ֵ�һ������������ABC�У�R��r�ֱ�Ϊ���Բ������Բ�İ뾶��O��I�ֱ�Ϊ�����ĺ����ģ���![]() .
.
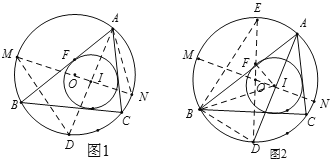
��ͼ1����O�͡�I�ֱ��ǡ�ABC�����Բ������Բ����I��AB���з��ڵ�F�����O�İ뾶ΪR����I�İ뾶Ϊr������O�����������ߴ�ֱƽ���ߵĽ��㣩������I��������������ƽ���ߵĽ��㣩֮��ľ���OI��d������d2��R2��2Rr��
�����Ǹö�����֤�����̣����֣���
�ӳ�AI����O�ڵ�D������I����O��ֱ��MN������DM��AN.
�ߡ�D=��N����DMI=��NAI(ͬ�����Ե�Բ�ܽ����)��
���MDI�ס�ANI��
��![]() ��
��
��![]() �٣�
�٣�
��ͼ2����ͼ1(��ȥMD��AN)�Ļ���������O��ֱ��DE������BE��BD��BI��IF��
��DE����O��ֱ�������DBE=90����
�ߡ�I��AB�����ڵ�F�����AFI=90����
���DBE=��IFA��
�ߡ�BAD=��E(ͬ������Բ�ܽ����)��
���AIF�ס�EDB��
��![]() ����
����![]() �ڣ�
�ڣ�
����(1)�۲췢�֣�![]() ��
��![]() (�ú�R��d�Ĵ���ʽ��ʾ)��
(�ú�R��d�Ĵ���ʽ��ʾ)��
(2)���ж�BD��ID��������ϵ����˵�����ɣ�
(3)��۲�ʽ�Ӣٺ�ʽ�Ӣڣ�����������(1)��(2)�Ľ��ۣ����������֤��˼·����ɸö���֤����ʣ�ಿ�֣�
(4)Ӧ�ã�����ABC�����Բ�İ뾶Ϊ5cm������Բ�İ뾶Ϊ2cm������ABC������������֮��ľ���Ϊ cm.

���𰸡�(1)R-d��(2)BD=ID�����ɼ�������(3)��������(4)![]() .
.
��������
(1)ֱ�ӹ۲�ɵã�
(2)�����������ĵ����ʿɵá�BAD=��CAD����CBI=��ABI����Բ�ܽǶ����ɵá�DBC=��CAD���ٸ�����������ǵ����ʼ�����á�BID=��DBI���̶���֤��BD=ID��
(3)Ӧ��(1)(2)���ۼ��ɣ�
(4)ֱ�Ӵ�����۽��м��㼴�ɣ�
(1)��O��I��N���㹲�ߣ�
��OI+IN��ON��
��IN��ON��OI��R��d��
�ʴ�Ϊ��R��d��
(2)BD=ID���������£�
����I����ABC�����ģ�
���BAD=��CAD����CBI=��ABI��
�ߡ�DBC=��CAD����BID=��BAD+��ABI����DBI=��DBC+��CBI��
���BID=��DBI��
��BD=ID��
(3)��(2)֪��BD=ID��
��![]() ��
��![]() ��
��
��DE��IF=IM��IN��
��![]() ��
��
��![]()
��![]() ��
��
(4)��(3)֪��![]() ��
��
��R=5��r=2����ã�![]() ��
��
��d>0��
��![]() ��
��
�ʴ�Ϊ��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C�ǡ�O�ϵ������㣬��D��BC���ӳ�����.�������ĸ����ۣ����ڡ�ABC���ԵĻ��ϴ���һ��E��ʹ�á�BCE=��DCE�����ڡ�ABC���ԵĻ��ϴ���һ��E��ʹ�á�BAE=��AEC�����ڡ�ABC���ԵĻ��ϴ���һ��E��ʹ��EOƽ�֡�AEC�����ڡ�ABC���ԵĻ�������ȡһ��E(�����A��C�غ�) ����DCE=��ABO +��AEO������.���������У�������ȷ���۵�����ǣ� ��

A. �٢ڢ� B. �٢ۢ� C. �ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��2ax��
��1�����κ���ͼ��ĶԳ�����ֱ��x���� ����
��2����0��x��3ʱ��y�����ֵ����Сֵ�IJ�Ϊ4����ö��κ����ı���ʽ��
��3����a��0�����ڶ��κ���ͼ���ϵ�����P��x1��y1����Q��x2��y2������t��x1��t+1��x2��3ʱ��������y1��y2�����Ϻ���ͼ��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���D��E�ֱ��ڱ�BC��AC�ϣ���CD=CE������DE���ӳ�����F��ʹEF=AE������AF��CF������BE���ӳ���CF�ڵ�G�����н��ۣ�
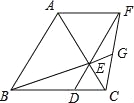
�١�ABE�ա�ACF����BC=DF����S��ABC=S��ACF+S��DCF������BD=2DC����GF=2EG��������ȷ�Ľ����� ������д������ȷ���۵���ţ�
���𰸡��٢ڢۢ�.
��������
���������������ABC�ǵȱ������Σ��ɵ�AB=AC=BC����BAC=��ACB=60�㣬����DE=DC�����ж���DEC�ǵȱ������Σ�����ED=EC=DC����DEC=��AEF=60�㣬
��EF=AE��������AEF�ǵȱ������Σ�����AF=AE����EAF=60�㣬�ڡ�ABE�͡�ACF�У�AB=AC,��BAE=��CAF,AE=AF �����ж���ABE�ա�ACF���ʢ���ȷ��������ABC=��FDC���ɵ�AB��DF��������EAF=��ACB=60�㣬�ɵ�AB��AF�������ж��ı���ABDF��ƽ���ı��Σ�����DF=AB=BC���ʢ���ȷ��������ABE�ա�ACF�ɵ�BE=CF��S��ABE=S��AFC���ڡ�BCE�͡�FDC�У�BC=DF,CE=CD,BE=CF �����ж���BCE�ա�FDC������S��BCE=S��FDC�����ɵ�S��ABC=S��ABE+S��BCE=S��ACF+S��BCE=S��ABC=S��ACF+S��DCF���ʢ���ȷ��������BCE�ա�FDC���ɵ���DBE=��EFG��������BED=��FEG���ж���BDE�ס�FGE������![]() =
=![]() ����
����![]() =
=![]() ������BD=2DC��DC=DE���ɵ�
������BD=2DC��DC=DE���ɵ�![]() =2����FG=2EG���ʢ���ȷ��
=2����FG=2EG���ʢ���ȷ��
���㣺�������ۺ���.
�����͡������
��������
19
����Ŀ���Ȼ�������ֵ��(a��1��![]() )��(
)��(![]() )������a��2��
)������a��2��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�A��B����������x���Ϸ�����C��������(��1��0)���Ե�CΪλ�����ģ���x����·�����ABC��λ��ͼ�Σ����ѡ�ABC�ı߳��Ŵ�ԭ����2�����õ���A'B'C'�����B�Ķ�Ӧ��B'�ĺ�����Ϊ2�����B�ĺ�����Ϊ(����)
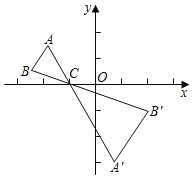
A.��1B.![]() C.��2D.
C.��2D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
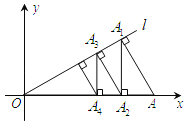
����Ŀ����ͼ������![]() ��ֱ��
��ֱ��![]() �Ĵ��ߣ�����Ϊ��
�Ĵ��ߣ�����Ϊ��![]() ������
������![]() ��
��![]() �ᣬ����Ϊ��
�ᣬ����Ϊ��![]() ������
������![]() ��
��![]() ��������
������Ϊ��![]() ��������������ȥ���õ�һ���߶�
��������������ȥ���õ�һ���߶�![]() �������߶�
�������߶�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AB=AC��AC����O�ڵ�E��BC����O�ڵ�D��F��CE���е㣬����DF�������н��۴������
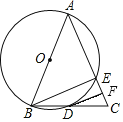
A.��A=��ABEB.![]()
C.BD=DCD.DF�ǡ�O������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ���������ඩ��һ����ѧ���������������ġ����̡�һ���һ�η�����������ﲼ�ö��ɵģ��������������е����ͼ�����ŵģ�Ϊ��ͼ���㣬���ǰ�����Ϊ���ţ���ͼ1��ͼ2��ͼ�и��д������г���������ֱ��ʾδ֪��x��y��ϵ������Ӧ�ij������ͼ1��ʾ�����ͼ��������������Ϥ�ķ�������ʽ��������������![]() �����Ƶأ�ͼ2��ʾ�����ͼ���ǿ��Ա���Ϊ��������
�����Ƶأ�ͼ2��ʾ�����ͼ���ǿ��Ա���Ϊ��������

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=��x+4�������ύ��A��B���㣬OC��AB�ڵ�C��P���߶�OC�ϵ�һ�����㣬����AP�����߶�AP�Ƶ�A��ʱ����ת45�㣬�õ��߶�AP'������CP'�����߶�CP'����СֵΪ(����)
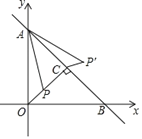
A.![]() B.1C.
B.1C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com