
【题目】如图1,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴相交于点
轴相交于点![]() ,对称轴与
,对称轴与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 相交于点
相交于点![]() .
.
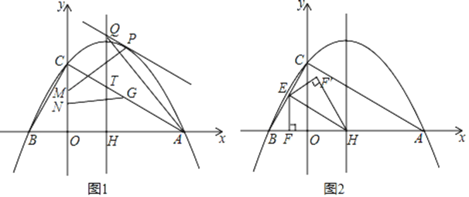
(1)点![]() 是线段
是线段![]() 上方抛物线上一点,过点
上方抛物线上一点,过点![]() 作
作![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,当
,当![]() 面积最大时,点
面积最大时,点![]() 、
、![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的上方),
的上方),![]() ,点
,点![]() 在直线
在直线![]() 上,求
上,求![]() 的最小值.
的最小值.
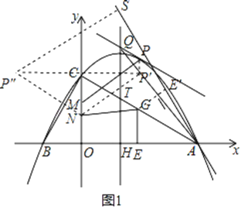
(2)点![]() 为
为![]() 中点,
中点,![]() 轴于
轴于![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得△
翻折得△![]() ,如图所示,再将△
,如图所示,再将△![]() 沿直线
沿直线![]() 平移,记平移中的△
平移,记平移中的△![]() 为△
为△![]() ,在平移过程中,直线
,在平移过程中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则是否存在这样的点
,则是否存在这样的点![]() ,使得△
,使得△![]() 为等腰三角形?若存在,求出
为等腰三角形?若存在,求出![]() 点坐标.
点坐标.
【答案】(1)![]() 的最小值为
的最小值为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)由抛物线解析式可求A(6,0),C(0,![]() ),对称轴x=2,过P点作PT′∥QT,由PQ∥AC可知,四边形QTT′P是平行四边形,QT=PT’,因为HT为定值,所以PT′最大时,△AQH面积最大,由此构建二次函数,求出点P坐标,过点G作GE⊥x轴于E,作x轴关于直线AC的对称直线l,E的对称点为E′,将PM沿y轴向下平移
),对称轴x=2,过P点作PT′∥QT,由PQ∥AC可知,四边形QTT′P是平行四边形,QT=PT’,因为HT为定值,所以PT′最大时,△AQH面积最大,由此构建二次函数,求出点P坐标,过点G作GE⊥x轴于E,作x轴关于直线AC的对称直线l,E的对称点为E′,将PM沿y轴向下平移![]() 个单位至P′N,作点P′关于y轴的对称点P″,过P″作P″S⊥l于S,则有PM+NG+
个单位至P′N,作点P′关于y轴的对称点P″,过P″作P″S⊥l于S,则有PM+NG+![]() GA=P″N+NG+GE′≥P″S,求出P″S即可;
GA=P″N+NG+GE′≥P″S,求出P″S即可;
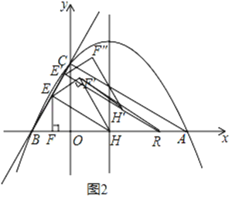
(2)先求得点E,F,F′,H′,R的坐标,根据△RF'H'为等腰三角形,分三种情况分别求解即可.
(1)如图1,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),
的右侧),
![]() ;
;![]() ;
;![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
![]()
过![]() 点作
点作![]() ,交
,交![]() 于
于![]() ,
,
设![]() ,
,![]() ,
,
则![]()
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
当![]() 面积最大时,
面积最大时,![]() 最大,即
最大,即![]() 最大,
最大,
即![]() 时,
时,![]() 面积最大,
面积最大,
此时![]() 点坐标为
点坐标为![]() .
.
过点![]() 作
作![]() 轴于
轴于![]() ,作
,作![]() 轴关于直线
轴关于直线![]() 的对称直线
的对称直线![]() ,
,![]() 的对称点为
的对称点为![]() ,将
,将![]() 沿
沿![]() 轴向下平移
轴向下平移![]() 个单位至
个单位至![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过
,过![]() 作
作![]() 于
于![]() ,则有
,则有
![]()
![]() ,
,![]() 与
与![]() 关于
关于![]() 轴对称
轴对称
![]() ,
,
![]() ,直线
,直线![]() 与
与![]() 轴关于直线
轴关于直线![]() 对称
对称
![]() ,
,
![]()
设直线![]() 的解析式为
的解析式为![]() ,则
,则![]()
![]() ,将
,将![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]()
![]()
过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() 轴
轴
![]()
![]()
![]()
![]() ,
,![]()
![]() 的最小值
的最小值![]() ;
;
(2)![]()
![]() 抛物线对称轴为直线
抛物线对称轴为直线![]() ,
,
![]() ,
,
由(1)知:![]() ;
;![]() ;
;![]() ,
,![]() ,
,
![]() 点
点![]() 为
为![]() 中点,
中点,![]() 轴于
轴于![]() ,
,
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() △
△![]() 沿直线
沿直线![]() 平移,各个点横纵坐标变化为
平移,各个点横纵坐标变化为![]() ,设△
,设△![]() 沿直线
沿直线![]() 平移后的△
平移后的△![]() 各顶点坐标分别为
各顶点坐标分别为
![]() ,
,![]()
则直线![]() 解析式为
解析式为![]() ,令
,令![]() ,则
,则![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() △
△![]() 为等腰三角形,
为等腰三角形,
![]() 或
或![]() 或
或![]() ,
,
①当![]() 时,则
时,则![]() ,解得:
,解得:![]() ,
,![]()
此时,![]() 或
或![]()
②当![]() 时,则
时,则![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 不符合题意,
不符合题意,![]() 与①重复
与①重复
③当![]() 时,
时,![]() ,解得:
,解得:![]() ,与①重复
,与①重复
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
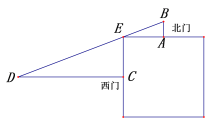
【题目】我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?” .其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B出有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,求正方形城池的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(m+1)x2﹣(m+3)x+2=0.
(1)证明:当m≠﹣1时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止.在甲车出发的同时,乙车也从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶.若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在两车出发后经过_____小时相遇.
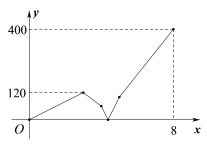
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2),现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
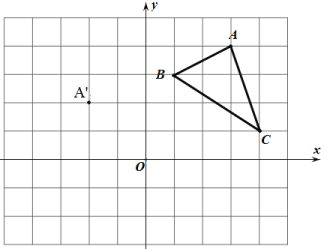
(1)直接写出点B'、C'的坐标:B' ,C' ;并在坐标系中画出平移后的△A'B'C'(不写画法);
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P的坐标是 ;
(3)若△ABC绕点C逆时针旋转90°至△A1B1C,画出△A1B1C.
(4)求△A'B'C'的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
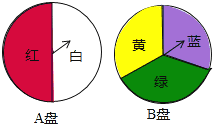
【题目】小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分 成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出 了蓝色,那么配成了紫色.
(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某二次函数图象的顶点坐标为(1,-4),且经过点C(0,-3)
(1)求这个二次函数的表达式;
(2)求图象与x轴交点A、B两点的坐标(A在点B的左边)及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.
(1)转动一次转盘,获得50元、30元、10元购物券的概率分别是多少?
(2)如果有一名顾客在商场消费了200元,通过计算说明转转盘和直接获得购物券,哪种方式对这位顾客更合算?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com