
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
【答案】C
【解析】
①根据全等三角形的判定方法,证出△ACD≌△BCE,即可得出AD=BE.
③先证明△ACP≌△BCQ,即可判断出CP=CQ,③正确;
②根据∠PCQ=60°,可得△PCQ为等边三角形,证出∠PQC=∠DCE=60°,得出PQ∥AE,②正确.
④没有条件证出BO=OE,得出④错误;
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,⑤正确;即可得出结论.
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,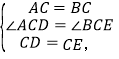
∴△ACD≌△BCE(SAS),
∴AD=BE,结论①正确,
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
又∵![]()
∴![]()
∴![]()
在△ACP和△BCQ中,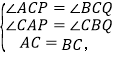
∴△ACP≌△BCQ(AAS),
∴CP=CQ,结论③正确;
又∵![]()
∴△PCQ为等边三角形,
∴![]()
∴PQ∥AE,结论②正确,
∵△ACD≌△BCE,
∴∠ADC=∠AEO,
∴![]()
∴结论⑤正确.没有条件证出BO=OE,④错误;
综上,可得正确的结论有4个:①②③⑤.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】a、b、c在数轴上的位置如图所示,则:
(1)用“<、>、=”填空:a____0,b____0,c_____0;
(2)用“<、>、=”填空:﹣a____0,a﹣b____0,c﹣a____0;
(3)化简:|﹣a|﹣|a﹣b|+|c﹣a|
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC放置在第一象限内,顶点A在x轴上,若顶点B的坐标是(4,3),(1)请求出菱形边长OA的长度.
(2)反比例函数![]() 经过点C,请求出
经过点C,请求出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给出四个命题:
①直角三角形的两边是方程y2-7y+12=0的两根,则它的第三边是5;
②若一元二次方程ax2+bx+c=0(a≠0)的系数a,c异号,则该方程有两个不相等的实数根;
③若一元二次方程(m-2)x2+x+m2-4=0有一个根为0,那么m=±2;
④已知一元二次方程ax2+bx+c=0(a≠0)中a,b,c满足a-b+c=0,4a+2b+c=0则方程的两根为x1=-1,x2=2;其中真命题的是__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD.(S表示面积)
实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+![]() .
.
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF=![]() ,求EG的长.
,求EG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
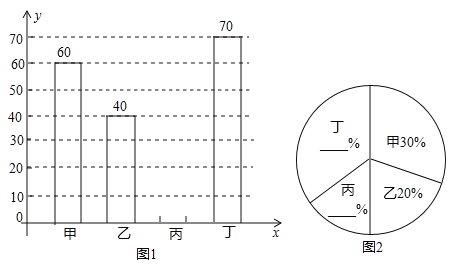
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
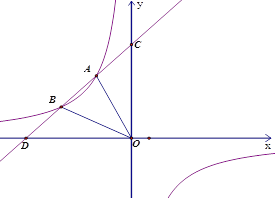
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com