
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解集.
的解集.
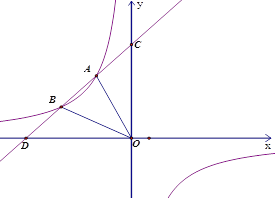
【答案】(1) ![]() ;(2) 6;(3) -4<x<-2或x>0
;(2) 6;(3) -4<x<-2或x>0
【解析】分析:(1)根据待定系数法就可以求出函数的解析式;
(2)求△AOB的面积就是求A,B两点的坐标,将一次函数与反比例函数的解析式组成方程即可求得;
(3)观察图象即可求得一次函数比反比例函数大的区间.
详解:(1)设一次函数解析式为y=kx+b,
∵一次函数与坐标轴的交点为(-6,0),(0,6),
∴![]() 解得:
解得: ![]() ,
,
∴一次函数关系式为:y=x+6,
∴B(-4,2),
∴反比例函数关系式为: ![]() ;
;
(2)∵点A与点B是反比例函数与一次函数的交点,
∴A(-2,4),
∴S△AOB=6×6÷2-6×2=6;
(3)-4<x<-2或x>0.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c=0;④若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可)
,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可) 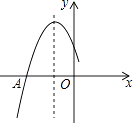
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
知识运用:
(1)如图1,表示0的点D到点A的距离是1,到点B的距离是2,那么点D 【A,B】的好点;(请在横线上填是或不是)
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数 所对应的点是【M,N】的好点(写出所有可能的情况);
拓展提升:
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过几秒时,P、A和B中恰有一个点为其余两点的好点?(写出所有情况)
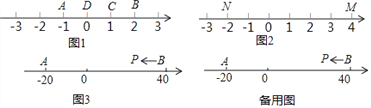
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点 A、B 所表示的数分别为 a 和 b,且满足|a+3|+(b-9)2018=0,O 为原点.
(1) 试求 a 和 b 的值
(2) 点 C 从 O 点出发向右运动,经过 3 秒后点 C 到 A 点的距离是点 C 到 B 点距离的 3 倍,求点 C 的运动速 度?
(3) 点 D 以 1 个单位每秒的速度从点 O 向右运动,同时点 P 从点 A 出发以 5 个单位每秒的速度向左运动, 点 Q 从点 B 出发,以 20 个单位每秒的速度向右运动.在运动过程中,M、N 分别为 PD、OQ 的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )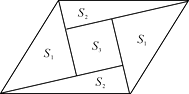
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年11月读书节,深圳市统计某学校九年级学生读书状况,制作了两幅不完整的统计图如图所示.
(1)x的值为 ,参加调查的总人数为 人;
(2)补全条形统计图;
(3)若全市有6.7万学生,则看3本及3本书以上的学生约有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com