
ЁОЬтФПЁПдФЖСРэНтЃК
ШєAЁЂBЁЂCЮЊЪ§жсЩЯШ§ЕуЃЌШєЕуCЕНAЕФОрРыЪЧЕуCЕНBЕФОрРы2БЖЃЌЮвУЧОЭГЦЕуCЪЧЁОAЃЌBЁПЕФКУЕуЃЎ
ШчЭМ1ЃЌЕуAБэЪОЕФЪ§ЮЊЉ1ЃЌЕуBБэЪОЕФЪ§ЮЊ2ЃЎБэЪО1ЕФЕуCЕНЕуAЕФОрРыЪЧ2ЃЌЕНЕуBЕФОрРыЪЧ1ЃЌФЧУДЕуCЪЧЁОAЃЌBЁПЕФКУЕуЃЎ
жЊЪЖдЫгУЃК
ЃЈ1ЃЉШчЭМ1ЃЌБэЪО0ЕФЕуDЕНЕуAЕФОрРыЪЧ1ЃЌЕНЕуBЕФОрРыЪЧ2ЃЌФЧУДЕуD ЁОAЃЌBЁПЕФКУЕуЃЛЃЈЧыдкКсЯпЩЯЬюЪЧЛђВЛЪЧЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌMЁЂNЮЊЪ§жсЩЯСНЕуЃЌЕуMЫљБэЪОЕФЪ§ЮЊ4ЃЌЕуNЫљБэЪОЕФЪ§ЮЊЉ2ЃЎЪ§ ЫљЖдгІЕФЕуЪЧЁОMЃЌNЁПЕФКУЕуЃЈаДГіЫљгаПЩФмЕФЧщПіЃЉЃЛ
ЭиеЙЬсЩ§ЃК
ЃЈ3ЃЉШчЭМ3ЃЌAЁЂBЮЊЪ§жсЩЯСНЕуЃЌЕуAЫљБэЪОЕФЪ§ЮЊЉ20ЃЌЕуBЫљБэЪОЕФЪ§ЮЊ40ЃЎЯжгавЛжЛЕчзгТьвЯPДгЕуBГіЗЂЃЌвд4ИіЕЅЮЛУПУыЕФЫйЖШЯђзѓдЫЖЏЃЌЕНДяЕуAЭЃжЙЃЎЕБОЙ§МИУыЪБЃЌPЁЂAКЭBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃПЃЈаДГіЫљгаЧщПіЃЉ
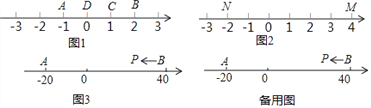
ЁОД№АИЁПЃЈ1ЃЉВЛЪЧЃЛЃЈ2ЃЉ0Лђ-8ЃЛЃЈ3ЃЉ5ЃЌ10ЃЌ7.5.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЖЈвхЗЂЯжЃККУЕуБэЪОЕФЪ§ЕНЁОAЃЌBЁПжаЃЌЧАУцЕФЕуAЪЧЕНКѓУцЕФЪ§BЕФОрРыЕФ2БЖЃЌДгЖјЕУГіНсТлЃЛ
ЃЈ2ЃЉЕуMЕНЕуNЕФОрРыЮЊ6ЃЌЗжШ§ЕШЗжЮЊЗнЮЊ2ЃЌИљОнЖЈвхЕУЃККУЕуЫљБэЪОЕФЪ§ЮЊ0Лђ-8ЃЛ
ЃЈ3ЃЉИљОнКУЕуЕФЖЈвхПЩжЊЗжСНжжЧщПіЃКЂйPЮЊЃЈAЃЌBЃЉЕФКУЕуЃЛЂкPЮЊЃЈBЃЌAЃЉЕФКУЕуЃЛЂлBЮЊЃЈAЃЌPЃЉЕФКУЕуЃЎЩшЕуPБэЪОЕФЪ§ЮЊxЃЌИљОнКУЕуЕФЖЈвхСаГіЗНГЬЃЌНјЖјЕУГіtЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1ЃЌЁпЕуDЕНЕуAЕФОрРыЪЧ1ЃЌЕНЕуBЕФОрРыЪЧ2ЃЌ
ИљОнКУЕуЕФЖЈвхЕУЃКDB=2DAЃЌ
ФЧУДЕуDВЛЪЧЁОAЃЌBЁПЕФКУЕу
ЃЈ2ЃЉШчЭМ2ЃЌ4-ЃЈ-2ЃЉ=6ЃЌ6ЁТ3ЁС2=4ЃЌ
МДОрРыЕуM4ИіЕЅЮЛЃЌОрРыЕуN2ИіЕЅЮЛЕФЕуОЭЪЧЫљЧѓЕФКУЕу0ЃЛ
ЁрЪ§0ЫљБэЪОЕФЕуЪЧЁОMЃЌNЁПЕФКУЕуЃЛ
4-ЃЈ-8ЃЉ=12ЃЌ-2-ЃЈ-8ЃЉ=6ЃЌ
ЭЌРэЃКЪ§-8ЫљБэЪОЕФЕувВЪЧЁОMЃЌNЁПЕФКУЕуЃЛ
ЁрЪ§0Лђ-8ЫљБэЪОЕФЕуЪЧЁОMЃЌNЁПЕФКУЕуЃЛ
ЃЈ3ЃЉЩшЕуPБэЪОЕФЪ§ЮЊxЃЌдђPA=x+20ЃЌPB=40-xЃЌAB=40-ЃЈ-20ЃЉ=60ЃЌ
ЗжШ§жжЧщПіЃК
ЂйPЮЊЃЈAЃЌBЃЉЕФКУЕуЃЎ
гЩЬтвтЃЌЕУPA=2PBЃЌМДx-ЃЈ-20ЃЉ=2ЃЈ40-xЃЉЃЌ
НтЕУx=20ЃЌ
Ёрt=ЃЈ40-20ЃЉЁТ4=5ЃЈУыЃЉЃЛ
ЂкPЮЊЃЈBЃЌAЃЉЕФКУЕуЃЎ
гЩЬтвтЃЌЕУPB=2PAЃЌМД40-x=2ЃЈx+20ЃЉЃЌ
НтЕУx=0ЃЌ
Ёрt=ЃЈ40-0ЃЉЁТ4=10ЃЈУыЃЉЃЛ
ЂлBЮЊЃЈAЃЌPЃЉЕФКУЕуЃЎ
гЩЬтвтЃЌЕУAB=2PAЃЌМД60=2ЃЈx+20ЃЉ
НтЕУx=10ЃЌ
ДЫЪБЃЌЕуPЮЊABЕФжаЕуЃЌМДAвВЮЊЃЈBЃЌPЃЉЕФКУЕуЃЌ
Ёрt=30ЁТ4=7.5ЃЈУыЃЉЃЛ
злЩЯПЩжЊЃЌЕБtЮЊ5УыЁЂ10УыЛђ7.5УыЪБЃЌPЁЂAКЭBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃЎ


 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБШНЯДѓаЁЃК
ЃЃЈ-3.5ЃЉ____ЉЃќЃ4.5ЃќЃЌ38.15Ёу_____ 38Ёу15ЁфЃЈЬюЁАЃОЁБЁАЃМЁБЛђЁА=ЁБЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=k1x+bЕФЭМЯѓОЙ§AЃЈ0ЃЌЉ2ЃЉЃЌBЃЈ1ЃЌ0ЃЉСНЕуЃЌгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓдкЕквЛЯѓЯоФкЕФНЛЕуЮЊMЃЈmЃЌ4ЃЉЃЎ
ЕФЭМЯѓдкЕквЛЯѓЯоФкЕФНЛЕуЮЊMЃЈmЃЌ4ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙAMЁЭMPЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ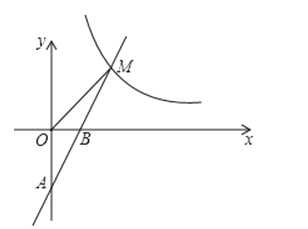
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЬЛЈГЇФГжжРёХкЕФЩ§ПеИпЖШhЃЈmЃЉгыЗЩааЪБМфtЃЈsЃЉЕФЙиЯЕЪНЪЧhЃНЉ2t2+20t+1ЃЌШєетжжРёХкдкЕуЛ№Щ§ПеЕНзюИпЕуДІв§БЌЃЌдђДгЕуЛ№Щ§ПеЕНв§БЌашвЊЕФЪБМфЮЊЃЈЁЁЁЁЃЉ
A.3sB.4sC.5sD.10s
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШЛЏМђЃЌдйЧѓжЕЃК(3a2-8a)+(2a3-13a2+2a)-2(a3-3)ЃЌЦфжаa=-4ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБШНЯДѓаЁЃКЉЃЈЉ5ЃЉЉЉ|Љ5|ЃЌЁАЉЁБжагІИУЬюЃЈЁЁЁЁЃЉ
A. ЃОB. ЃМC. ЃНD. ЮоЗЈБШНЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ8ЗжЃЉдкЪ§жсЩЯЃЌ
ЃЈ1ЃЉШчЙћЕуAБэЪОЪ§2ЃЌЖЏЕуBДгЕуAГіЗЂЯђзѓвЦЖЏ5ИіЕЅЮЛГЄЖШЃЌдйЯђгввЦЖЏ8ИіЕЅЮЛГЄЖШЃЌДЫЪБЕуBБэЪОЕФЪ§ЪЧ ЃЌAЁЂBСНЕуМфЕФОрРыЪЧ ЃЛ
ЃЈ2ЃЉвЛАуЕФЃЌШчЙћЕуAБэЪОЪ§ЮЊaЃЌЖЏЕуBДгЕуAГіЗЂЯђгввЦЖЏbИіЕЅЮЛГЄЖШЃЌдйЯђзѓвЦЖЏcИіЕЅЮЛГЄЖШЃЌДЫЪБЕуBБэЪОЕФЪ§ЪЧ ЃЌAЃЎBСНЕуМфЕФОрРыЪЧ ЃЈгУaЁЂbЁЂcЕФЪНзгБэЪОЃЉЃЎ
ЃЈ3ЃЉШчЙћЕуAБэЪОЪ§Ѓ4 ЃЌЕуBБэЪОЕФЪ§ЪЧ8ЃЌФЧУДAЁЂBСНЕуМфЕФОрРыЪЧ ЃЌABЕФжаЕуЫљБэЪОЕФЪ§ЪЧ ЃЛ
ЃЈ4ЃЉвЛАуЕиЃЌШчЙћЕуAБэЪОЕФЪ§ЮЊaЃЌЕуBБэЪОЕФЪ§ЪЧbЃЌФЧУДAЁЂBСНЕуМфЕФОрРыЪЧ ЃЌABЕФжаЕуБэЪОЕФЪ§ЪЧ ЃЈгУaЁЂbЕФЪНзгБэЪОЃЉЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A. АДНЧЗжРрЃЌШ§НЧаЮПЩвдЗжЮЊЖлНЧШ§НЧаЮЁЂШёНЧШ§НЧаЮКЭЕШбќжБНЧШ§НЧаЮ
B. АДБпЗжРрЃЌШ§НЧаЮПЩЗжЮЊЕШбќШ§НЧаЮЁЂВЛЕШБпШ§НЧаЮКЭЕШБпШ§НЧаЮ
C. Ш§НЧаЮЕФЭтНЧДѓгкШЮКЮвЛИіФкНЧ
D. вЛИіШ§НЧаЮжажСЩйгавЛИіФкНЧВЛДѓгк60Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
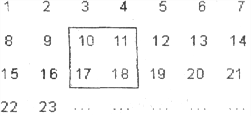
ЁОЬтФПЁПАбе§ећЪ§1ЃЌ2ЃЌ3ЃЌ4ЃЌЁЁЃЌ2009ХХСаГЩШчЭМЫљЪОЕФвЛИіБэ
ЃЈ1ЃЉгУвЛе§ЗНаЮдкБэжаЫцвтПђзЁ4ИіЪ§ЃЌАбЦфжазюаЁЕФЪ§МЧЮЊxЃЌСэШ§ИіЪ§гУКЌxЕФЪНзгБэЪОГіРДЃЌДгаЁЕНДѓвРДЮЪЧ ЃЌ ЃЌ ЁЃ
ЃЈ2ЃЉЕББЛПђзЁЕФ4ИіЪ§жЎКЭЕШгк416ЪБЃЌxЕФжЕЪЧЖрЩй?
ЃЈ3ЃЉБЛПђзЁЕФ4ИіЪ§жЎКЭФмЗёЕШгк622ЃПШчЙћФмЃЌЧыЧѓГіДЫЪБxЕФжЕЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com