
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c=0;④若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可)
,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可) 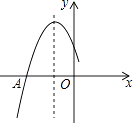
【答案】①③④
【解析】解:由函数图象可知抛物线与x轴有2个交点, ∴b2﹣4ac>0即b2>4ac,故①正确;
∵对称轴为直线x=﹣1,
∴﹣ ![]() =﹣1,即2a﹣b=0,故②错误;
=﹣1,即2a﹣b=0,故②错误;
∵抛物线与x轴的交点A坐标为(﹣3,0)且对称轴为x=﹣1,
∴抛物线与x轴的另一交点为(1,0),
∴将(1,0)代入解析式可得,a+b+c=0,故③正确;
∵a<0,
∴开口向下,
∵|﹣ ![]() +1|=
+1|= ![]() ,|﹣
,|﹣ ![]() +1=
+1= ![]() ,
,
∴y1<y2 , 故④正确;
综上,正确的结论是:①③④,
所以答案是①③④.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,菱形OABC放置在第一象限内,顶点A在x轴上,若顶点B的坐标是(4,3),(1)请求出菱形边长OA的长度.
(2)反比例函数![]() 经过点C,请求出
经过点C,请求出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
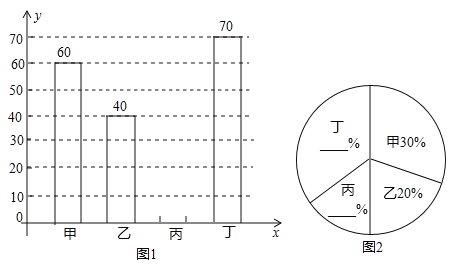
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(﹣2,0),点B(0,﹣4),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,8)、C(4,b).
经过C,D两点且D(a,8)、C(4,b).
(1)求a、b、k的值;
(2)如图2,点P在双曲线y=![]() 上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
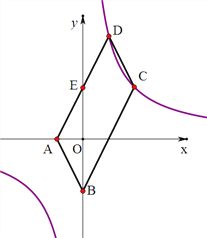
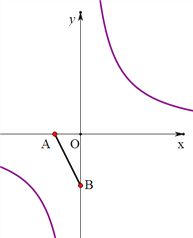
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点. 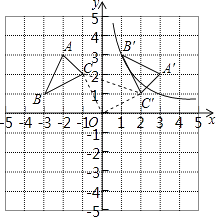
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
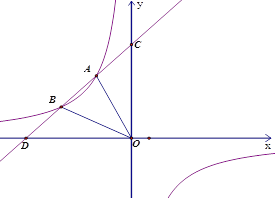
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD、C′D′分别是Rt△ABC,Rt△A′B′C′斜边上的高,且CB=C′B′,CD=C′D′.求证:△ABC≌△A′B′C′.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com