
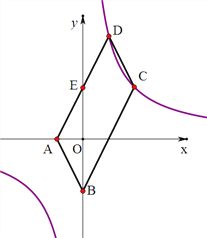
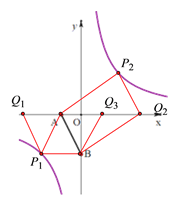
【题目】如图1,已知点A(﹣2,0),点B(0,﹣4),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,8)、C(4,b).
经过C,D两点且D(a,8)、C(4,b).
(1)求a、b、k的值;
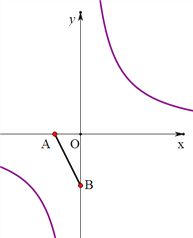
(2)如图2,点P在双曲线y=![]() 上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
【答案】(1) a=2,k=16,b=4;(2) Q1(6,0)或Q1(-6,0)Q1(2,0).
【解析】分析:
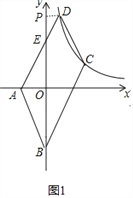
(1)如下图,过点D作DP⊥y轴于点P,结合已知条件可证得△PDE≌△OAE,由此可得PD==a=OA=2,这样即可得到点D的坐标,将点D的坐标代入![]() 中即可求得k的值,再结合点C(4,b)在该反比例函数的图象上即可求得b的值;
中即可求得k的值,再结合点C(4,b)在该反比例函数的图象上即可求得b的值;
(2)如下图,分AB为所求平行四边形的边和对角线两种情况结合已知条件分析讨论即可.
(1)如图1,过点D作DP⊥y轴于点P,
∵点E为AD的中点,
∴AE=DE.
又∵DP⊥y轴,∠AOE=90°,
∴∠DPE=∠AEO.
∵在△PDE与△OAE中,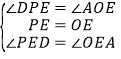 ,
,
∴△PDE≌△OAE(ASA),
∴PD=OA,
∵A(﹣2,0),
∴a=2,
∴D(2,8).
∵点D在反比例函数图象上,
∴k=xy=2×8=16.
∵点C在反比例函数图象上,C的坐标为(4,b),
∴b=![]() =4,
=4,
∴a=2,k=16,b=4;
(2)∵点P在双曲线![]() 上,点Q在x轴上,
上,点Q在x轴上,
∴可设点P的坐标为![]() ,点Q的坐标为(m,0),
,点Q的坐标为(m,0),
如下图,①当AB为所求平行四边形ABP1Q1的边时,由点B的坐标为(0,-4)可得点P此时的坐标(-4,-4),∴PB=AQ1=4,
∴OQ1=OA+AQ1=6,
∴此时点Q1的坐标为(-6,0);
②当AB为所求平行四边形ABQ2P2的边时,由平行四边形的性质可知点P到x轴的距离=点B到x轴的距离=4,
∴点P此时的坐标为(4,4);
又∵点P可以可知是由点A平移得到的,而点Q2可以看着是由点B平移得到的,
∴由平移的性质可得点Q2的坐标为(6,0);
③当AB为所求平行四边形AP1BQ3的对角线时,由AQ3=PB结合①中所得PB=4可得AQ3=4,
∵AO=2,
∴OQ3=4-2=2,
∴Q3的坐标为(2,0);
综上所述,满足条件的点Q有3个,坐标分别为:Q1(-6,0)或Q2(6,0)或Q3(2,0).


科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE;连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,
求证:BM=DM且BM⊥DM;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
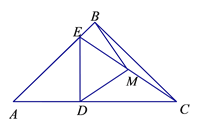

图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣ ![]() x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成道路的长度分别是多少m?
(2)若村委每天需付给甲队的道路改造费用为0.4万元,乙队为0.25万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c=0;④若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可)
,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可) 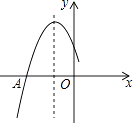
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况,随机抽取部分市民进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.
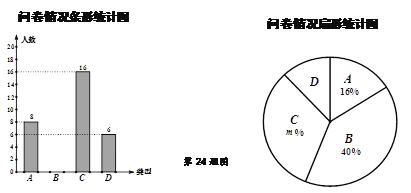
(1)本次问卷共随机调查了 名市民,扇形统计图中![]() .
.
(2)请根据数据信息补全条形统计图.
(3)扇形统计图中“D类型”所对应的圆心角的度数是 .
(4)从这次接受调查的市民中随机抽查一个,恰好是“不了解”的概率是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
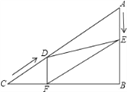
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com