
【题目】已知数轴上两点 A、B 所表示的数分别为 a 和 b,且满足|a+3|+(b-9)2018=0,O 为原点.
(1) 试求 a 和 b 的值
(2) 点 C 从 O 点出发向右运动,经过 3 秒后点 C 到 A 点的距离是点 C 到 B 点距离的 3 倍,求点 C 的运动速 度?
(3) 点 D 以 1 个单位每秒的速度从点 O 向右运动,同时点 P 从点 A 出发以 5 个单位每秒的速度向左运动, 点 Q 从点 B 出发,以 20 个单位每秒的速度向右运动.在运动过程中,M、N 分别为 PD、OQ 的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
【答案】(1)a=-3,b=9;(2)2或5.(3)不发生变化;理由见解析.
【解析】
(1)根据非负数的性质求得a、b的值即可;(2)设C速度为x,则3秒后C点所表示的数为3x,根据数轴上两点之间的距离列方程即可得出答案;(3)设运动时间为t,根据速度可求出t秒时P、D、Q、M、N的位置,求出PQ、OD、MN的距离,进而求出![]() 的值即可得答案.
的值即可得答案.
(1)∵|a+3|+(b-9)2018=0,
∴a+3=0,b-9=0,
解得:a=-3,b=9;
(2)设C速度为x,则3秒后C点所表示的数为3x,
∴∣AC∣=3∣BC∣,即∣3x-(-3)∣=3∣9-3x∣,
解得:x=2或x=5,
故C的速度为:2或5.
(3)不发生变化;理由如下:
设运动时间为t,根据题意得:
P点的位置为:-3-5t ,
D点的位置为:t ,
Q点的位置为:9+20t,
M点的位置为:t-![]() =
=![]() ,
,
N点的位置为:![]() ,
,
∴PQ=9+20t-(-3-5t)=12+25t;OD =t;MN=![]() -
-![]() =6+12t;
=6+12t;
∴![]() =
=![]() =2,
=2,
故![]() 的值不发生变化.
的值不发生变化.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点. 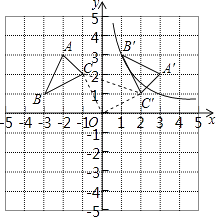
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
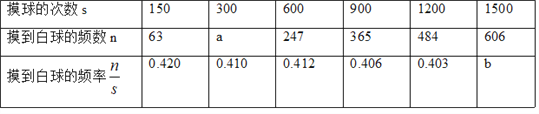
(1)按表格数据格式,表中的a= ;b= ;
(2)请估计:当次数s很大时,摸到白球的频率将会接近 ;
(3)请推算:摸到红球的概率是 (精确到0.1);
(4)试估算:口袋中红球有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
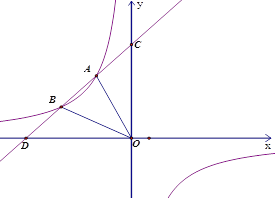
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.点A的纵坐标为4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早晨,小明步行到离家900米的学校去上学,到学校时发现眼镜忘在家中,于是他立即按原路步行回家,拿到眼镜后立即按原路骑自行车返回学校.已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟,小明骑自行车速度是步行速度的3倍.
(1)求小明步行速度(单位:米/分)是多少;
(2)下午放学后,小明骑自行车回到家,然后步行去图书馆,如果小明骑自行车和步行的速度不变,小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍,那么小明家与图书馆之间的路程最多是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:13=1=![]() ;13+23=9=
;13+23=9=![]() ;13+23+33=36=
;13+23+33=36=![]() ;13+23+33+43=100=
;13+23+33+43=100=![]() ,
,
回答下面的问题:
(1)13+23+33+43+…+103=_____(写出算式即可);
(2)计算13+23+33+…+993+1003的值;
(3)计算:113+123+…+993+1003的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+7+(﹣6)+(﹣7)
(2)(-20)+(+3)-(-5)-(+7)
(3)(﹣3.5)×(﹣2)÷(- ![]() )÷(﹣5)
)÷(﹣5)
(4)﹣14+16÷(﹣2)3×|﹣3﹣1|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com