
【题目】问题呈现:如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD.(S表示面积)
实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+![]() .
.
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF=![]() ,求EG的长.
,求EG的长.

【答案】问题呈现:证明见解析;实验探究:结论:2S四边形EFGH=S矩形ABCD﹣![]() ;(3)
;(3)![]() .
.
【解析】试题分析:只要说明S△HGE=![]() S矩形AEGD,同理S△EGF=
S矩形AEGD,同理S△EGF=![]() S矩形BEGC,由此可得S四边形EFGH=S△HGE+S△EFG=
S矩形BEGC,由此可得S四边形EFGH=S△HGE+S△EFG=![]() S矩形ABCD;
S矩形ABCD;
实验探究:结论:2S四边形EFGH=S矩形ABCD-S矩形A1B1C1D1.根据S△EHC1=![]() S矩形AEC1H,S△HGD1=
S矩形AEC1H,S△HGD1=![]() S矩形HDGD1,S△EFB1=
S矩形HDGD1,S△EFB1=![]() S矩形EBFB1,S△FGA1=
S矩形EBFB1,S△FGA1=![]() S矩形CFA1G,即可证明;
S矩形CFA1G,即可证明;
迁移应用:利用探究的结论即可解决问题.
试题解析:
如图中,

∵四边形ABCD是矩形,
∴AB∥CD,∠A=90°,
∵AE=DG,
∴四边形AEGD是矩形,
∴S△HGE=![]() S矩形AEGD,
S矩形AEGD,
同理S△EGF=![]() S矩形BEGC,
S矩形BEGC,
∴S四边形EFGH=S△HGE+S△EFG=![]() S矩形ABCD.
S矩形ABCD.
故答案为:S四边形EFGH=![]() S矩形ABCD.
S矩形ABCD.
实验探究:结论:2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1.

理由:∵S△EHC1=![]() S矩形AEC1H,S△HGD1=
S矩形AEC1H,S△HGD1=![]() S矩形HDGD1,S△EFB1=
S矩形HDGD1,S△EFB1=![]() S矩形EBFB1,S△FGA1=
S矩形EBFB1,S△FGA1=![]() S矩形CFA1G,
S矩形CFA1G,
∴S四边形EFGH=S△EHC1+S△HGD1+S△EFB1+S△FGA1﹣S矩形A1B1C1D1,
∴2S四边形EFGH=2S△EHC1+2S△HGD1+2S△EFB1+2S△FGA1﹣2S矩形A1B1C1D1,
∴2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1.
故答案为:2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1
迁移应用:解:(1)如图中,

∵2S四边形EFGH=S矩形ABCD﹣S矩形A1B1C1D1.
∴S矩形A1B1C1D1=25﹣2×9=7=A1B1A1D1,
∵正方形的面积为25,
∴边长为5,
∵A1D12=HF2﹣52=29﹣25=4,
∴A1D1=2,A1B1=![]() ,
,
∴EG2=A1B12+52=![]() ,
,
∴EG=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
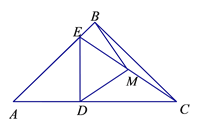
【题目】已知:在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE;连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,
求证:BM=DM且BM⊥DM;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.

图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣ ![]() x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com