【题目】古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案科目：初中数学 来源： 题型：
【题目】计算：
（1）45+（-22）+（-8）-（-5）；（2）（－4
）－（－5
）+（－4）－3
；
(3)
÷
； (4)－14＋|3－5|－16÷(－2)×．
查看答案和解析>>
科目：初中数学 来源： 题型：
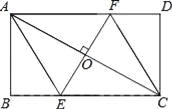
【题目】如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．
（1）求证：四边形AECF是菱形；
（2）若AB=
，∠DCF=30°，求四边形AECF的面积．（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
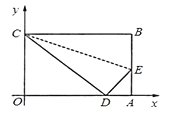
【题目】如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，A点坐标为（10, 0），C点坐标为（0, 6），将边BC折叠，使点B落在边OA上的点D处，求线段EA 的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3），△AOB绕点O逆时针旋转90°后得到△A1OB1 ．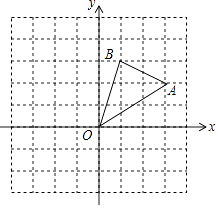 
（1）点A关于点O中心对称的点P的坐标为；
（2）在网格内画出△A1OB1；
（3）点A1、B1的坐标分别为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】a、b、c在数轴上的位置如图所示，则：
（1）用“＜、＞、＝”填空：a____0，b____0，c_____0；
（2）用“＜、＞、＝”填空：﹣a____0，a﹣b____0，c﹣a____0；
（3）化简：|﹣a|﹣|a﹣b|+|c﹣a|
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，对角线AC、BD交于点O．M为AD中点，连接CM交BD于点N，且ON=1．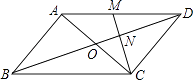 
（1）求BD的长；
（2）若△DCN的面积为2，求四边形ABNM的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知 m≥2，n≥2，且 m、n 均为正整数，如果将 mn 进行如图所示的“分解”，那么下列四个叙述中正确的有（ ）
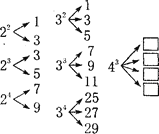
①在 25 的“分解”结果是 15和17两个数．
②在 42 的“分解”结果中最大的数是9．
③若 m3 的“分解”结果中最小的数是 23，则 m＝5．
④若 3n 的“分解”结果中最小的数是 79，则 n＝5．
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题呈现：如图1，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上，AE=DG，求证：2S四边形EFGH=S矩形ABCD．（S表示面积）
实验探究：某数学实验小组发现：若图1中AH≠BF，点G在CD上移动时，上述结论会发生变化，分别过点E、G作BC边的平行线，再分别过点F、H作AB边的平行线，四条平行线分别相交于点A1、B1、C1、D1，得到矩形A1B1C1D1．
如图2，当AH＞BF时，若将点G向点C靠近（DG＞AE），经过探索，发现：2S四边形EFGH=S矩形ABCD+
．
如图3，当AH＞BF时，若将点G向点D靠近（DG＜AE），请探索S四边形EFGH、S矩形ABCD与之间的数量关系，并说明理由．
迁移应用：
请直接应用“实验探究”中发现的结论解答下列问题：
如图4，点E、F、G、H分别是面积为25的正方形ABCD各边上的点，已知AH＞BF，AE＞DG，S四边形EFGH=11，HF=
，求EG的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
