
分析 首先设AP=x,然后表示出BP=5-x,利用已知的等积式得到CP2=x(50-x),然后在△ACP中,根据余弦定理得到CP2=AC2+AP2-2AC•APcosA=900+x2-60x×0.6,从而得到有关x的方程9+x2-6x•0.6=x(5-x),解之即可.
解答 解:∵∠ACB=90°,AC=30,BC=40,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=50,
设AP=x,则BP=50-x,CP2=x(50-x),
在△ACP中,根据余弦定理有
CP2=AC2+AP2-2AC•APcosA=900+x2-60x×0.6,
则有900+x2-60x•0.6=x(50-x),
整理,得x2-43x+45=0
解得:x=25或x=18
∴CP=25或CP=$\sqrt{AP•PB}$=$\sqrt{18×32}$=24,
故答案为24或25.
点评 本题考查了相似三角形的判定与性质,初中教材中已经将余弦定理的内容删掉,解题时可以借助网络等渠道了解余弦定理.


科目:初中数学 来源: 题型:选择题
| A. | |-2|=-2 | B. | a2•a3=a6 | C. | (-3)-2=$\frac{1}{9}$ | D. | $\sqrt{12}$=3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
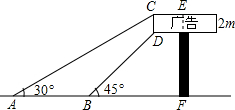 如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)
如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处
如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处查看答案和解析>>
科目:初中数学 来源: 题型:选择题
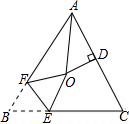 如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.
如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.| A. | 108 | B. | 120 | C. | 126 | D. | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
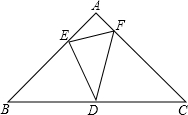 已知△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上,点E在AB上,点F在AC上,∠EDF=45°.
已知△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上,点E在AB上,点F在AC上,∠EDF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com