
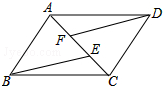
 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
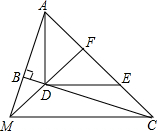 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.查看答案和解析>>
科目:初中数学 来源: 题型:
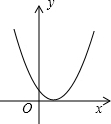 二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是( )
二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号实数根 |
| C、有两个相等的实数 |
| D、无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:
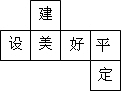 2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )
2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、好 | C、平 | D、定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
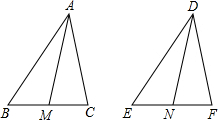
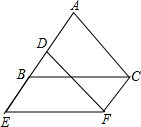 如图,△DEF是由△ABC沿AB方向平移2cm得到的,已知△ABC的周长为22cm,则四边形AEFC的周长为( )
如图,△DEF是由△ABC沿AB方向平移2cm得到的,已知△ABC的周长为22cm,则四边形AEFC的周长为( )| A、22cm | B、24cm |
| C、26cm | D、28cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
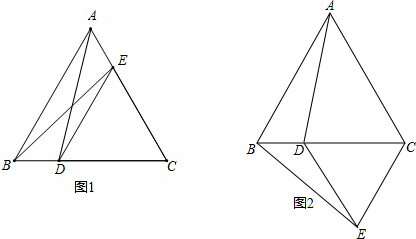
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com