练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
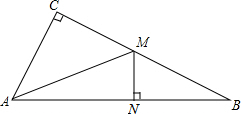
    1．如图，在Rt△ABC中，∠C=90，AM是中线，MN⊥AB，垂足为点N，求证：AN2-BN2=AC2．

    分析 在直角三角形BNM和ANM中利用勾股定理可以得到BN2=BM2-MN2，AN2=AM2-MN2，然后得到BN2-AN2=（BM2-MN2）-（AM2-MN2）=BM2-AM2；又在直角三角形AMC中，AM2=AC2+CM2，代入前面的式子中即可得出结论．

    解答 证明：∵MN⊥AB于N，
    ∴BN2=BM2-MN2，AN2=AM2-MN2
    ∴BN2-AN2=BM2-AM2，
    又∵∠C=90°，
    ∴AM2=AC2+CM2
    ∴BN2-AN2=BM2-AC2-CM2，
    又∵BM=CM，
    ∴BN2-AN2=-AC2，
    即AN2-BN2=AC2．

    点评 本题考查了勾股定理、三角形的中线；熟练掌握勾股定理，并能进行推理论证是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

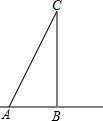    11．如图，B村在A村的正东方向6千米处，自来水公司的水处理厂（用C点表示）恰好在B村的正北方向．现要从C处向两村铺设管道输送自来水，经测量．从C到A村的距离比到B村的距离多2千米．求B村到水处理厂的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．化简：$\frac{2}{3\sqrt{5}}$=$\frac{2\sqrt{5}}{15}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知三角形两边长分别为3和6，第三边的数值是一元二次方程（x-5）2-4=0的两个根，试求三角形的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图所示，点A表示的数是数D的相反数，点C表示的数与点B表示的数互为相反数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知α，β是方程2x2-3x+1=0的两个根，则α+β=$\frac{3}{2}$，α•β=$\frac{1}{2}$，α2β+αβ2=$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列各数中．是有理数的是（　　）
    A．面积为3的正方形的边长
    B．体积为8的正方体的棱长
    C．两直角边分别为2和3的直角三角形的斜边长
    D．长为3，宽为2的长方形的对角线长

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．若x1、x2是一元二次方程-2x2+3x+1=0的两个根，求下列代数式的值．
    （1）$（{x}_{1}-{x}_{2}）^{2}$
    （2）$\frac{{x}_{2}}{{x}_{1}}+\frac{{x}_{1}}{{x}_{2}}$
    （3）（x1-2）（x2-2）
    （4）|x1-x2|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．若|x+2|+|y+3|=0，求2x2-y+1的值．

    查看答案和解析>>

    同步练习册答案