
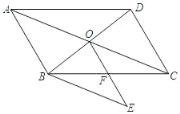
【题目】如图,在□ABCD中,AC与BD相交于点O,过点B作BE∥AC,联结OE交BC于点F,点F为BC的中点.
(1)求证:四边形AOEB是平行四边形;
(2)如果∠OBC=∠E,求证:BOOC=ABFC.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据BE∥AC,△COF∽△BEF,又因为F为BC的中点可得CF=BF,所以BE=OC=OA,结合BE∥AC,即可证得AOEB是平行四边形.
(2)根据题意可证得△COB∽△CBA,即![]() ,在依据AC=2OC,BC=2FC,可得
,在依据AC=2OC,BC=2FC,可得![]() ,即可证得BOOC=ABFC
,即可证得BOOC=ABFC
(1)∵BE∥AC,
∴△COF∽△BEF
∴![]()
∵点F为BC的中点,
∴CF=BF,
∴OC=BE
∵四边形ABCD是平行四边形,
∴AO=CO
∴AO=BE
∵BE∥AC,
∴四边形AOEB是平行四边形
(2)∵四边形AOEB是平行四边形,
∴∠BAO=∠E
∵∠OBC=∠E,
∴∠BAO=∠OBC
∵∠ACB=∠BCO,
∴△COB∽△CBA
∴![]()
∵四边形ABCD是平行四边形,
∴AC=2OC
∵点F为BC的中点,
∴BC=2FC
∴![]()
即BOOC=ABFC.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠A=90°,AB=AC=4![]() ,D、E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
,D、E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
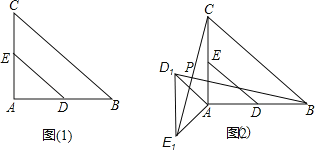
(1)求证:BD1=CE1;
(2)当∠CPD1=2∠CAD1时,则旋转角为α= (直接写结果)
(3)连接PA,△PAB面积的最大值为 (直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ΔABC中,AB=AC,若将ΔABC绕点C顺时针180得到ΔFEC。

(1)试猜想AE与BF有何关系,并说明理由;
(2)若ΔABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为上![]() 一点,且BE=CF,
一点,且BE=CF,
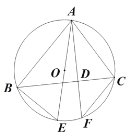
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=4,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 、
、![]() ,将线段
,将线段![]() 绕着原点
绕着原点![]() 逆时针方向旋转角度
逆时针方向旋转角度![]() 到
到![]() ,连接
,连接![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针方向旋转角度
顺时针方向旋转角度![]() 至
至![]() ,连接
,连接![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
(3)已知![]() ,当
,当![]() 时,改变
时,改变![]() 的大小,求
的大小,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
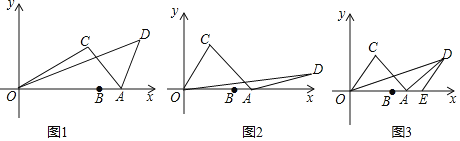
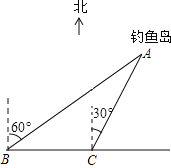
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点![]() 和点
和点![]() ,给出如下定义:若
,给出如下定义:若![]() ,则称点
,则称点![]() 为点
为点![]() 的限变点.例如:点
的限变点.例如:点![]() 的限变点的坐标是
的限变点的坐标是![]() ,点
,点![]() 的限变点的坐标是
的限变点的坐标是![]() .
.
(1)①点![]() 的限变点的坐标是___________;
的限变点的坐标是___________;
②在点![]() ,
,![]() 中有一个点是函数
中有一个点是函数![]() 图象上某一个点的限变点,这个点是_______________;
图象上某一个点的限变点,这个点是_______________;
(2)若点![]() 在函数
在函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若点![]() 在关于
在关于![]() 的二次函数
的二次函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() 或
或![]() ,其中
,其中![]() .令
.令![]() ,求
,求![]() 关于
关于![]() 的函数解析式及
的函数解析式及![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com