
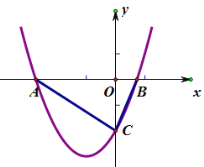
【题目】已知抛物线y=![]() x2-mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
x2-mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .若
.若![]() ,
,![]() .
.
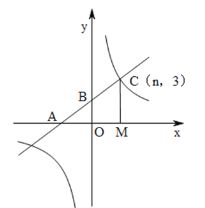
(1)求反比例函数和一次函数的解析式;
(2)当![]() 时,求x的取值范围。
时,求x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
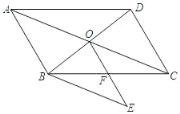
【题目】如图,在□ABCD中,AC与BD相交于点O,过点B作BE∥AC,联结OE交BC于点F,点F为BC的中点.
(1)求证:四边形AOEB是平行四边形;
(2)如果∠OBC=∠E,求证:BOOC=ABFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
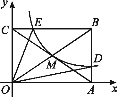
①![]() ;②连接MD,S△ODM=2S△OCE,;③
;②连接MD,S△ODM=2S△OCE,;③![]() ;④连接
;④连接![]() ,则△BED∽△BCA.
,则△BED∽△BCA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
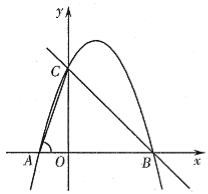
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.
(1)求抛物线的解析式;
(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2-(m+3)y+![]() (5m2-2m+13)=0 (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)=0 (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
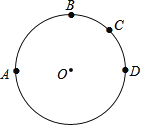
【题目】如图所示A、B、C、D四点在⊙O上的位置,其中![]() =180°,且
=180°,且![]() =
=![]() ,
,![]() =
=![]() .若阿超在
.若阿超在![]() 上取一点P,在
上取一点P,在![]() 上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
A. Q点在![]() 上,且
上,且![]() >
>![]() B. Q点在
B. Q点在![]() 上,且
上,且![]() <
<![]()
C. Q点在![]() 上,且
上,且![]() >
>![]() D. Q点在
D. Q点在![]() 上,且
上,且![]() <
<![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com