
【题目】如图,反比例函数![]() 的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
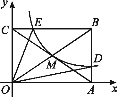
①![]() ;②连接MD,S△ODM=2S△OCE,;③
;②连接MD,S△ODM=2S△OCE,;③![]() ;④连接
;④连接![]() ,则△BED∽△BCA.
,则△BED∽△BCA.
【答案】①③④
【解析】
①正确.由四边形ABCD是矩形,推出S△OBC=S△OBA,由点E、点D在反比例函数y=![]() (x>0)的图象上,推出S△CEO=S△OAD=
(x>0)的图象上,推出S△CEO=S△OAD=![]() ,即可推出S△OEB=S△OBD.
,即可推出S△OEB=S△OBD.
②错误.因为![]() b=
b=![]() ab,所以S△ODM:S△OCE=
ab,所以S△ODM:S△OCE=![]() ,故错误.
,故错误.
③正确.设点B(m,n),D(m,n′)则M(![]() m,
m,![]() n,),由点M,点D在反比例函数y=
n,),由点M,点D在反比例函数y=![]() (x>0)的图象上,可得
(x>0)的图象上,可得![]() m
m![]() n=mn′,推出n′=
n=mn′,推出n′=![]() n,推出AD=
n,推出AD=![]() AB,推出BD=3AD,故正确.
AB,推出BD=3AD,故正确.
④正确.由![]() =3,推出DE∥AC,推出△BED∽△BCA.
=3,推出DE∥AC,推出△BED∽△BCA.
∵四边形ABCD是矩形,
∴S△OBC=S△OBA,
∵点E、点D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴S△CEO=S△OAD=![]() ,
,
∴S△OEB=S△OBD,故①正确;
连接DM,∵S△ODM=S△OBD﹣S△BDM=![]() ,
,
∵S△CEO=S△OAD=![]() ,
,
∴S△ODM:S△OCE=![]() ,故②错误;
,故②错误;
设点B(m,n),D(m,n′)则M(![]() m,
m,![]() n,),
n,),
∵点M,点D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴![]() m
m![]() n=mn′,
n=mn′,
∴n′=![]() n,
n,
∴AD=![]() AB,
AB,
∴BD=3AD,故③正确;
连接DE,同法可证CE=![]() BC,
BC,
∴BE=3EC,
∴![]() ,
,
∴DE∥AC,
∴△BED∽△BCA,故④正确.
故答案是:①③④.


科目:初中数学 来源: 题型:
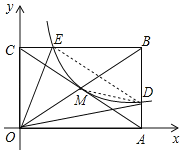
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
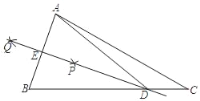
【题目】如图,在锐角△ABC中,小明进行了如下的尺规作图:
①分别以点A、B为圆心,以大于![]() AB的长为半径作弧,两弧分别相交于点P、Q;
AB的长为半径作弧,两弧分别相交于点P、Q;
②作直线PQ分别交边AB、BC于点E、D.
(1)小明所求作的直线DE是线段AB的 ;
(2)联结AD,AD=7,sin∠DAC=![]() ,BC=9,求AC的长.
,BC=9,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种商品,每件商品的成本为![]() 元,经市场调查发现,在一段时间内,销售量
元,经市场调查发现,在一段时间内,销售量![]() (件)随销售单价
(件)随销售单价![]() (元/件)的变化而变化,具体关系式为
(元/件)的变化而变化,具体关系式为![]() ,设这种商品在这段时间内的销售利润为
,设这种商品在这段时间内的销售利润为![]() (元),解答如下问题:
(元),解答如下问题:
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 取何值时,
取何值时,![]() 的值最大?
的值最大?
(3)如果物价部门规定这种商品的销售单价不得高于![]() 元/件,公司想要在这段时间内获得
元/件,公司想要在这段时间内获得![]() 元的销售利润,那么销售单价应定为多少?
元的销售利润,那么销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是( )

A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格![]() (元/公斤)与第
(元/公斤)与第![]() 天之间满足
天之间满足![]() (
(![]() 为正整数),销售量
为正整数),销售量![]() (公斤)与第
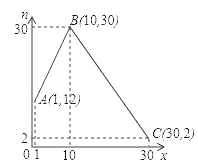
(公斤)与第![]() 天之间的函数关系如图所示:
天之间的函数关系如图所示:
如果李大爷的草莓在上市销售期间每天的维护费用为80元.
(1)求销售量![]() 与第
与第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)求在草莓上市销售的30天中,每天的销售利润![]() 与第
与第![]() 天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
(3)求日销售利润![]() 的最大值及相应的
的最大值及相应的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com