
【题目】如图,正方形![]() 中,
中,![]() 经顺时针旋转后与
经顺时针旋转后与![]() 重合.
重合.

(1)旋转中心是点 ,旋转了 度;
(2)如果![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)A,90;(2)![]() .
.
【解析】
(1)根据正方形的性质得AB=AD,∠BAD=90°,则根据旋转的定义得到△ADE绕点A顺时针旋转90°后与△ABF重合;
(2)根据旋转的性质得BF=DE,S△ABF=S△ADE,利用CF=CB+BF=8得到BC+DE=8,再加上CE=CD-DE=BC-DE=4,于是可计算出BC=6,于是得到结论.
解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,
即旋转中心是点A,旋转了90度;
故答案为A,90;
(2)∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴BF=DE,S△ABF=S△ADE,
而CF=CB+BF=8,
∴BC+DE=8,
∵CE=CD-DE=BC-DE=4,
∴BC=6,
∴AC=![]() BC=6
BC=6![]() .
.
故答案为:(1)A,90;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为_____.
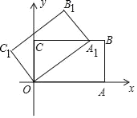
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h= m
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
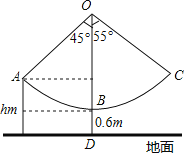
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.
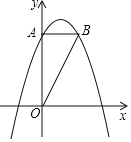
(1)求抛物线的解析式.
(2)将△OAB绕点O顺时针旋转90°得到△OA'B',试判断B'是否落在抛物线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,以点A为圆心,2为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,则线段AF的长的最小值____.![]()
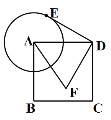
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
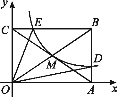
①![]() ;②连接MD,S△ODM=2S△OCE,;③
;②连接MD,S△ODM=2S△OCE,;③![]() ;④连接
;④连接![]() ,则△BED∽△BCA.
,则△BED∽△BCA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com