
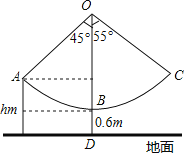
����Ŀ��ij��ũ����������һ����ǧ��������ͼ��ʾ����ǧ����OB�ij�Ϊ3m����ֹʱ��̤�嵽�������BD�ij�Ϊ0.6m��̤���Ⱥ��Բ��ƣ���Ϊ��ȫ��������������涨����ͯ������ȫ�߶���Ϊhm�����˵�����ȫ�߶���Ϊ2m����������ȷ��0.1m��
��1��������OA��OB��45���н�ʱ��ǡΪ��ͯ�İ�ȫ�߶ȣ���h���� ��m
��2��ij����������ǧʱ������OC��OB�����н�Ϊ55�����ʴ����Ƿ�ȫ�����ο����ݣ�![]() ��1.41��sin55���0.82��cos55���0.57��tan55���1.43��
��1.41��sin55���0.82��cos55���0.57��tan55���1.43��
���𰸡���1��1.5����2�������ǰ�ȫ�ģ�
��������
��1���������Ҷ��������OE���ٸ���AF=OB+BD�����DE�����ɵó�h��ֵ��
��2����C����CM��DF����DF�ڵ�M��������֪���������Ҷ������OE���ٸ���CM=OB+DE-OE�����CM��������˵�����ȫ�߶������бȽϣ����ɵó��𰸣�
�⣺��1����Rt��ANO�У���ANO��90����
��cos��AON��![]() ��
��
��ON��OAcos��AON��
��OA��OB��3m����AON��45����
��ON��3cos45���2.12m��
��ND��3+0.6��2.12��1.5m��
��h��ND��AF��1.5m��
�ʴ�Ϊ1.5��
��2����ͼ����C����CM��DF����DF�ڵ�M��
��Rt��CEO����CEO��90����
��cos��COE��![]() ��
��
��OE��OCcos��COF��
��OB��OC��3m����CON��55����
��OE��3cos55���1.72m��
��ED��3+0.6��1.72��1.9m��
��CM��ED��1.9m��
�߳��˵�����ȫ�߶���Ϊ2m��
������ǰ�ȫ�ģ�



 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
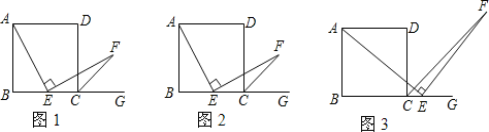
����Ŀ����ѧ����,����ʦ��ʾ�����⣺��ͼ1,�ı���ABCD��������,��E�DZ�BC���е�.��AEF=90������EF����������ǡ�DCG��ƽ����CF�ڵ�F����֤��AE=EF.
����˼��,С��չʾ��һ����ȷ�Ľ���˼·����AB�Ͻ�ȡBM=BE,����ME����AM=EC,��֤��AME�ա�ECF������AE=EF.
�ڴ˻����ϣ�ͬѧ�����˽�һ�����о���
(1)Сӱ�������ͼ2,���������E�DZ�BC���е�����Ϊ����E�DZ�BC��(��B,C��)������һ�����������������䣬��ô������AE=EF����Ȼ����������ΪСӱ�Ĺ۵���ȷ��?�����ȷ��д��֤�����̣��������ȷ����˵�����ɣ�
(2)С���������ͼ3,��E��BC���ӳ�����(��C����)������һ�㣬�����������䣬������AE=EF����Ȼ����������ΪС���Ĺ۵���ȷ��?�����ȷ��д��֤�����̣��������ȷ����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��
��1����ͼ1��E��G�ֱ���OB��OC�ϵĵ㣬CE��DG���ӳ����ཻ�ڵ�F����DF��CE����֤��OE��OG��
��2����ͼ2��H��BC�ϵĵ㣬����H��EH��BC�����߶�OB�ڵ�E������DH��CE�ڵ�F����OC�ڵ�G����OE��OG��
����֤����ODG����OCE��
����AB��1ʱ����HC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��2x2+8x��6��x�ύ�ڵ�A��B������������x�ἰ���Ϸ��IJ��ּ���C1����C1����ƽ�Ƶ�C2��C2��x�ύ�ڵ�B��D����ֱ��y=x+m��C1��C2����3����ͬ�Ľ��㣬��m��ȡֵ��Χ�ǣ�������

A. ��2��m��![]() B. ��3��m����
B. ��3��m����![]() C. ��3��m����2 D. ��3��m����
C. ��3��m����2 D. ��3��m����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
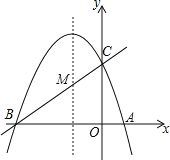
����Ŀ����ͼ����֪������y��ax2+bx+c(a��0)�ĶԳ���Ϊֱ��x����1���������߾���A(1��0)��C(0��3)���㣬��x�ύ�ڵ�B��
(1)��ֱ��y��mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
(2)�������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
(3)���PΪ�����ߵĶԳ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ź��������������������Σ�������������������ȫ�ȵģ�����ˮλʱ�����ˮ�����Ϊ![]() �������ˮ��
�������ˮ��![]() ��С�����ˮ��
��С�����ˮ��![]() ����ˮλ���Ǹպ���ûС��ʱ�����ˮ�����Ϊ________
����ˮλ���Ǹպ���ûС��ʱ�����ˮ�����Ϊ________![]() ��
��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
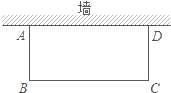
����Ŀ��У�յ�����һ��ǽ������Ϊ20m���ó�Ϊ32m����ʺ�����ǽΧ��һ�����λ��ԣ���ͼ��ʾ��
��1����Χ�������126m2�ľ��λ��������ܣ������˵���������ܣ���˵�����ɣ�
��2�������������4m��Χ�ɵľ��λ�������ܴﵽ170m2����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ��˳ʱ����ת����
��˳ʱ����ת����![]() �غ�.
�غ�.

��1����ת�����ǵ� ����ת�� �ȣ�
��2�����![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������y=��x2+4����2��x��2��ΪC1����x�ύ��A0��A1���㣬����ΪD1����C1�Ƶ�A1��ת180���õ�C2������ΪD2��C1��C2���һ���µ�ͼ��ֱ��y���ֱ��l����ͼ���ڵ�P1��x1��y1����P2��x2��y2�������߶�D1D2���ڵ�P3��x3��y3������x1��x2��x3��Ϊ������t=x1+x2+x3����t��ȡֵ��Χ�ǣ�������

A. 6��t��8 B. 6��t��8 C. 10��t��12 D. 10��t��12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com