
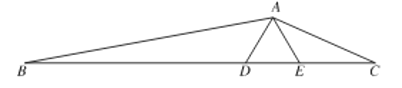
【题目】若![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上的两点,
上的两点,![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】16.5
【解析】
作![]() ,求出CH和AC的长,作EF⊥AD于点F,作AG∥EF交BC于点G,,通过证明△ABC∽GAC,可求出BC的值,从而可求出BD的值.
,求出CH和AC的长,作EF⊥AD于点F,作AG∥EF交BC于点G,,通过证明△ABC∽GAC,可求出BC的值,从而可求出BD的值.
解:作![]() ,
,
∵![]() ,且
,且![]() ,
,
∴△ADE是等边三角形,
∴DH=HE=![]() DE=
DE=![]() ,∠ADE=∠AED=∠DAE=60°,
,∠ADE=∠AED=∠DAE=60°,
∴CH=![]() +5=
+5=![]() ,AH==sin60°×AD=
,AH==sin60°×AD=![]() ,
,
∴AC=![]() .
.

作EF⊥AD于点F,作AG∥EF交BC于点G,
则∠AEF=∠DEF=30°,AF=DF,
∴∠AGC=150°,GE=DE=3,
∴CG=2,
∵![]() ,
,
∴∠BAC=∠AGC,
∵∠C=∠C,
∴△ABC∽GAC,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() ,
,
∴BD=![]() -3-5=16.5.
-3-5=16.5.
故答案为:16.5.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
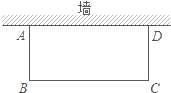
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为上![]() 一点,且BE=CF,
一点,且BE=CF,
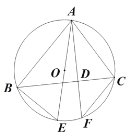
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=4,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
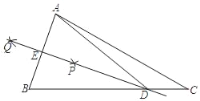
【题目】如图,在锐角△ABC中,小明进行了如下的尺规作图:
①分别以点A、B为圆心,以大于![]() AB的长为半径作弧,两弧分别相交于点P、Q;
AB的长为半径作弧,两弧分别相交于点P、Q;
②作直线PQ分别交边AB、BC于点E、D.
(1)小明所求作的直线DE是线段AB的 ;
(2)联结AD,AD=7,sin∠DAC=![]() ,BC=9,求AC的长.
,BC=9,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是( )

A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12
查看答案和解析>>
科目:初中数学 来源: 题型:
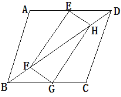
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com