
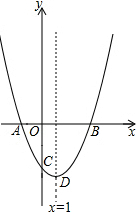
 已知二次函数图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点是点D,其中A(-1,0),C(0,-3),对称轴是直线x=1.
已知二次函数图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点是点D,其中A(-1,0),C(0,-3),对称轴是直线x=1.分析 (1)直接利用待定系数法求出二次函数解析式即可;
(2)利用当D与E点重合时,△ABE的面积S=8,符合题意的点有3个,进而得出△ABE的面积S>8,以及0<S<8时,E的个数;
(3)将四边形分割成三角形,进而表示出图形面积,再利用二次函数最值求法得出答案;
(4)利用QB⊥BC以及QC⊥CB时,分别利用勾股定理求出答案.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{a-b+c=0}\\{c=-3}\\{-\frac{b}{2a}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$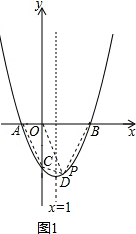
故二次函数的解析式为:y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
即D(1,-4),
当D,E点重合时,S△ABE=$\frac{1}{2}$×4×4=8,
故S=8时,E点有3个,x上方有2个,x轴下方有1个,共计3个;
S>8时,E点在x轴上方共有2个,
0<S<8时,x上方有2个,x轴下方有2个,共计4个;
(3)如图1,P(x,x2-2x-3)(0<x<3)
S四边形ABPC=S△AOC+S△POC+S△POB,
=$\frac{1}{2}×1×3+\frac{1}{2}×3×x+\frac{1}{2}×3×$(x2-2x-3),
=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{75}{8}$,
当x=$\frac{3}{2}$时,S最大值=$\frac{75}{8}$,此时P($\frac{3}{2}$,-$\frac{15}{4}$);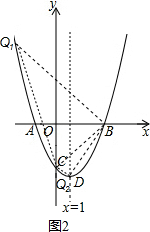
(4)如图2,Q(x,x2-2x-3),B(3,0),C(0,-3),
则BC2=18,BQ2=(x-3)2+(x2-2x-3)2,
QC2=x2+(x2-2x)2,
①QC2=BC2+BQ2,(x2-2x)2=18+(x-3)2+(x2-2x-3)2,
解得:x1=-2,x2=3,
x1=-2时,Q1(-2,5),x2=3时,与B重合,舍去,
②BQ2=BC2+QC2,(x-3)2+(x2-2x-3)2=18+x2+(x2-2x)2,
解得:x3=0,x4=1,
当x3=0时,与C重合,舍去,
当x4=1时,Q2(1,-4),
综上所述:Q1(-2,5)、Q2(1,-4).
点评 本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征以及不规则图形面积的求法等二次函数综合题型.解答(4)题时,利用分类讨论得出是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
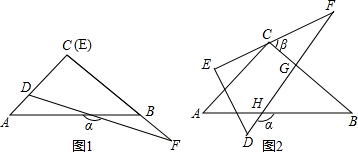
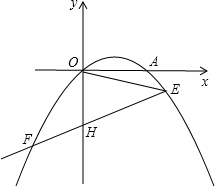 已知抛物线y=-$\frac{1}{3}$x2+$\frac{2}{3}$x经过原点,抛物线与x轴交于另一点A,点E(3,m)在抛物线上,连接OE,作∠OEF=45°,交抛物线于点F,求直线EF的解析式.
已知抛物线y=-$\frac{1}{3}$x2+$\frac{2}{3}$x经过原点,抛物线与x轴交于另一点A,点E(3,m)在抛物线上,连接OE,作∠OEF=45°,交抛物线于点F,求直线EF的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
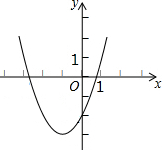 抛物线y=ax2+bx+c的顶点为D(-1,-3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①abc>0;②a+b+c<0;③a-c=3;④方程以ax2+bx+c+3=0有两个的实根,其中正确的个数为( )
抛物线y=ax2+bx+c的顶点为D(-1,-3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①abc>0;②a+b+c<0;③a-c=3;④方程以ax2+bx+c+3=0有两个的实根,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
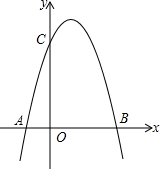 如图,二次函数的图象经过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.
如图,二次函数的图象经过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com