
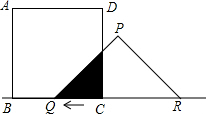
 如图,有一边长为5的正方形ABCD和一等腰△PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重叠部分的面积为S.
如图,有一边长为5的正方形ABCD和一等腰△PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重叠部分的面积为S.分析 (1)根据PE⊥QR,得出FC∥PE,即可证出△QCF∽△QEP;
(2)当t=5秒时,先根据△QFB∽△QPE,△RCG∽△REP,求出S△QFB、S△RCG,最后根据S=S△PRQ-S△QFB-S△RCG代入计算即可;
(3)当8≤t<9时,根据QB:QE=(t-5):4,△QFB∽△QPE,求出S△QFB,再根据S=S△PEQ-S△QFB代入计算即可;
(4)当9<t≤13时,根据RB:RE=(13-t):4,△RFB∽△RPE,求出S△RFB,再根据S=S△RFB把所得结果进行整理即可.
解答 解:(1)如图1: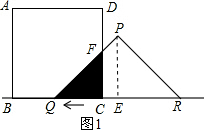
∵PQ=PR,点E为QR的中点,
∴PE⊥QR,
∴FC∥PE,
∴△QCF∽△QEP;
(2)当t=5时,CR=3.
设PR与DC交于G,∵PE⊥BC,PQ=PR=5,QR=8,
∴PE=$\sqrt{P{R}^{2}+R{E}^{2}}$=3,
由△RCG∽△REP,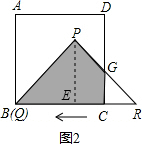
∴$\frac{CG}{PE}=\frac{CR}{RE}$,
∴CG=$\frac{9}{4}$,
∴S△RCG=$\frac{1}{2}$×3×$\frac{9}{4}$=$\frac{27}{8}$,
∴S=12-$\frac{27}{8}$=$\frac{69}{8}$(cm2);
(3)如图3: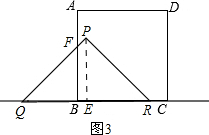 当8≤t<9时,
当8≤t<9时,
则QB:QE=(t-5):4,
∵△QFB∽△QPE,
∴S△QFB:S△QPE=(t-5)2:16,
∴S△QFB:6=(t-5)2:16,
∴S△QFB=$\frac{3}{8}$(t-5)2,
∴S=S△PEQ-S△QFB=12-$\frac{3}{8}$(t-5)2=-$\frac{3}{8}$t2+$\frac{15}{4}$+$\frac{21}{8}$,
如图4: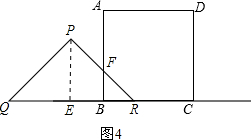
当9<t≤13时,
则RB:RE=(13-t):4,
∵△RFB∽△RPE,
∴S△RFB:S△RPE=(13-t)2:16,
∴S△RFB:6=(13-t)2:16,
∴S=S△RFB=$\frac{3}{8}$(13-t)2=$\frac{3}{8}$t2-$\frac{39}{4}$+$\frac{507}{8}$.
点评 此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、相似三角形的面积之比等于相似比的平方、等腰三角形的性质,关键是根据题意画出图形,注意分类讨论思想的运用.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,2) | B. | (-3,-2) | C. | (2,-2) | D. | (-1,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com