
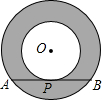
 如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )
如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
分析 连结OP、OA,如图,根据切线的性质得OP⊥AB,则利用垂径定理得到AP=BP=$\frac{1}{2}$AB=2$\sqrt{3}$,在Rt△OAP中利用勾股定理得到OA2-OP2=AP2=12,则(OA-OP)(OA+OP)=12,然后利用OA、OP为整数和整数的整除性解得$\left\{\begin{array}{l}{OA=4}\\{OP=2}\end{array}\right.$,于是可判断满足条件的不全等的“圆环带”有1个.
解答 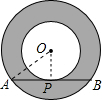 解:连结OP、OA,如图,
解:连结OP、OA,如图,
∵大圆的弦AB与小圆相切于点P,
∴OP⊥AB,
∴AP=BP=$\frac{1}{2}$AB=2$\sqrt{3}$,
在Rt△OAP中,OA2-OP2=AP2=(2$\sqrt{3}$)2=12,
∴(OA-OP)(OA+OP)=12,
而OA、OP为整数,
∴$\left\{\begin{array}{l}{OA-OP=1}\\{OA+OP=12}\end{array}\right.$或$\left\{\begin{array}{l}{OA-OP=2}\\{OA+OP=6}\end{array}\right.$或$\left\{\begin{array}{l}{OA-OP=3}\\{OA+OP=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{OA=4}\\{OP=2}\end{array}\right.$,
∴满足条件的不全等的“圆环带”有1个,即大圆半径为4,小圆半径为2.
故选A.
点评 本题考查了切线性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:解答题
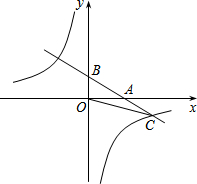 如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为$\sqrt{3}$.
如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
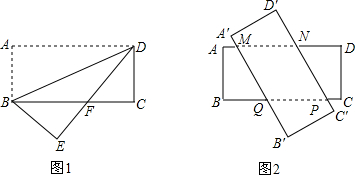
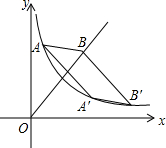 如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,设点B的横坐标为m,试用m的式子表示出点B′的坐标,并求出m的值.
如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,设点B的横坐标为m,试用m的式子表示出点B′的坐标,并求出m的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
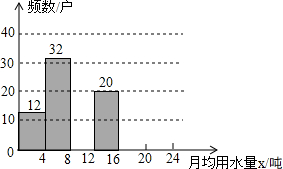 2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.| 月均用水量x(吨) | 频数(户) | 频率 |
| 0<x≤4 | 12 | a |
| 4<x≤8 | 32 | 0.32 |
| 8<x≤12 | b | c |
| 12<x≤16 | 20 | 0.2 |
| 16<x≤20 | 8 | 0.08 |
| 20<x≤24 | 4 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com