
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
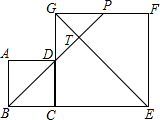 如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.
如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
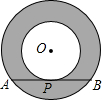 如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )
如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x>3}\\{x<1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x<5}\\{2x-1<9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-1>3}\\{y+2<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-1>3}\\{x-3<2}\\{2x-1<5}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com