
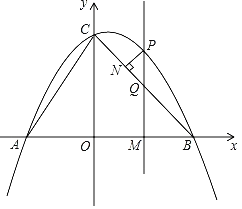
【题目】如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m.
(1)求此抛物线的表达式;
(2)过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由;
(3)过点P作PN⊥BC,垂足为点N.请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
【答案】(1)![]() (2)存在,点Q的坐标为:Q(1,3)或(
(2)存在,点Q的坐标为:Q(1,3)或(![]() ,
,![]() );(3)PN=﹣
);(3)PN=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,当m=2时,PN的最大值为
,当m=2时,PN的最大值为![]() .
.
【解析】
(1)由二次函数交点式表达式,即可求解;
(2)分AC=AQ、AC=CQ、CQ=AQ三种情况,利用方程或方程组求解即可得到答案;
(3)利用等腰直角三角形的性质得到:PN=PQsin∠PQN=![]() 即可求解.
即可求解.
解:(1)![]() 抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,
抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,
设![]()
即:﹣12a=4,解得:![]()
则抛物线的表达式为![]()
(2)存在,理由:
![]()
![]()
![]() 点A、B、C的坐标分别为(﹣3,0)、(4,0)、(0,4),
点A、B、C的坐标分别为(﹣3,0)、(4,0)、(0,4),
则AC=5,AB=7,BC=![]() ,∠OBC=∠OCB=45°,
,∠OBC=∠OCB=45°,
将点B、C的坐标代入一次函数表达式:y=kx+b并解得:y=﹣x+4…①,
同理可得直线AC的表达式为:![]() ,
,
①当AC=AQ时,如图1,
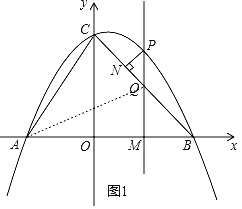
则AC=AQ=5,
设:QM=MB=n,则AM=7﹣n,
由勾股定理得:![]()
解得:n=3或4(舍去4),
故点Q(1,3);
②当AC=CQ时,如图1,
CQ=5,则BQ=BC﹣CQ=![]()
则QM=MB=![]() ,
,
故点Q(![]() ,
,![]() );
);
③当CQ=AQ时,则![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
设直线AC的中点为K(![]() ,2),
,2),
过点![]() 与CA垂直直线的表达式中的k值为
与CA垂直直线的表达式中的k值为![]() ,
,
直线![]() 的表达式为:
的表达式为:![]() ②,
②,
联立①②并解得:![]() (舍去);
(舍去);
故点Q的坐标为:Q(1,3)或(![]() ,
,![]() );
);
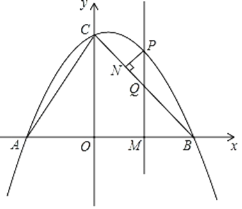
(3)设点![]() ,则点Q(m,﹣m+4),
,则点Q(m,﹣m+4),
∵OB=OC,∴∠ABC=∠OCB=45°=∠PQN,
PN=PQsin∠PQN=![]()
∵![]()
∴PN有最大值,
当m=2时,PN的最大值为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某电工想换房间的灯泡,已知灯泡到地面的距离为![]() ,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,
,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,![]() .设梯子一边
.设梯子一边![]() 与地面的夹角为
与地面的夹角为![]() ,且
,且![]() 可调节的范围为
可调节的范围为![]() .当
.当![]() 时,电工站在梯子安全挡中最高一档踏板
时,电工站在梯子安全挡中最高一档踏板![]() 上的最大触及高度为
上的最大触及高度为![]() .
.
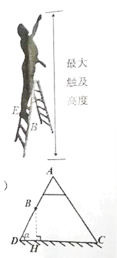
(1)当![]() 时,求踏板
时,求踏板![]() 离地面的高度
离地面的高度![]() .(精确到
.(精确到![]() )
)
(2)调节角度,试判断电工是否可以换下灯泡,并说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
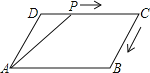
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=5,BC=3,点P从点D出发,沿DC,CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与AD,AP所围成的图形的面积为y,y随x的变化而变化.在下列图象中,能正确反映y与x的函数关系的是( )
A.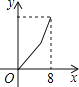 B.
B. C.
C.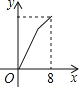 D.
D.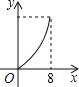
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
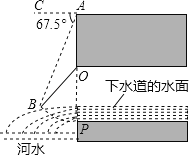
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
(![]() =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
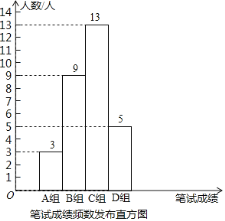
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续![]() 天的最低气温(单位:℃):
天的最低气温(单位:℃):![]() .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )
A.平均数是![]() B.中位数是
B.中位数是![]() C.众数是
C.众数是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
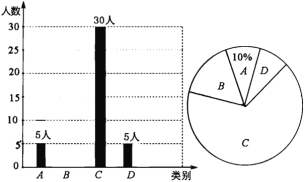
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com