
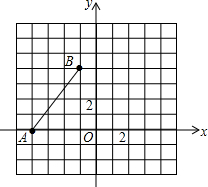
 如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.
如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.分析 (1)先利用旋转的性质,借助网格线画出点A′(0,4),点B′(4,1),然后利用待定系数法求出直线A′B′的解析式;
(2)利用待定系数法求出抛物线的解析式,再利用配方法得到抛物线顶点坐标,接着求出抛物线与一次函数的交点坐标,然后运用描点法画出抛物线;
(3)根据函数图象,找出直线A′B′不在抛物线下方所对应的自变量的取值范围即可.
解答 解:(1)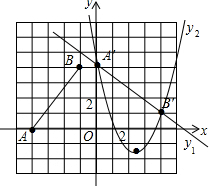 如图,点A′的坐标为(0,4),点B′的坐标为(4,1),
如图,点A′的坐标为(0,4),点B′的坐标为(4,1),
把A′(0,4),点B′(4,1)代入y1=mx+n得$\left\{\begin{array}{l}{n=4}\\{4m+n=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{3}{4}}\\{n=4}\end{array}\right.$,
所以直线A′B′的解析式为y1=-$\frac{3}{4}$x+4;
(2)把A′(0,4),点B′(4,1)代入y2=ax2-19cx+16c得$\left\{\begin{array}{l}{16c=4}\\{16a-19c×4+16c=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{c=\frac{1}{4}}\end{array}\right.$,
所以抛物线解析式为y2=x2-$\frac{19}{4}$x+4,
y2=x2-$\frac{19}{4}$x+4=(x-$\frac{19}{8}$)2-$\frac{105}{64}$,抛物线的顶点坐标为($\frac{19}{8}$,-$\frac{105}{64}$),
解方程组$\left\{\begin{array}{l}{y=-\frac{3}{4}x+4}\\{y={x}^{2}-\frac{19}{4}x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
所以直线A′B′与抛物线相交于点A′(0,4)和点B′(4,1),
如图;
(3)当0≤x≤4时,y1≥y2.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了待定系数法求函数解析式和二次函数与不等式(组).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
| 植树品种 | A种 | B种 | C种 | D种 |
| 植树棵数 | 150 | 125 | 125 |

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
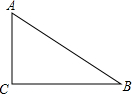 如图,在△ABC中,∠C=90°,那么点A到BC的距离是AC的长度,点B到AC的距离是BC的长度,点A,B两点的距离是AB的长度,三个距离最短的是AC,理由:垂线段最短.
如图,在△ABC中,∠C=90°,那么点A到BC的距离是AC的长度,点B到AC的距离是BC的长度,点A,B两点的距离是AB的长度,三个距离最短的是AC,理由:垂线段最短.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com