
����Ŀ���ס��������ֱ��A��B����ͬʱ�������׳�����ǰ��B�أ�����B����������һ�ٶȰ�ԭ·���ٷ��ص�A�أ��ҳ�����ǰ��A�أ���ס���������A�ص�·��Ϊy��ǧ�ף����׳���ʻ��ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ
��1����׳���A�ص���B�ص���ʻʱ�䣻
��2����׳�����ʱy��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3�����ҳ�����A��ʱ�׳���A�ص�·����
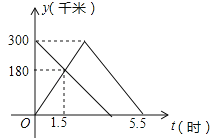
���𰸡���1��2.5����2��y=��100x+550��2.5��x��5.5������3��175��
��������
�����������1��������������ʽ���ɵõ����ۣ�
��2�����������з����鼴�ɵõ����ۣ�
��3��������������ʽ���ɵõ����ۣ�
�����������1��300�£�180��1.5��=2.5��Сʱ����
�𣺼׳���A�ص���B�ص���ʻʱ����2.5Сʱ��
��2����׳�����ʱy��x֮��ĺ�����ϵʽΪy=kx+b����![]() ����ã�
����ã�![]() ����׳�����ʱy��x֮��ĺ�����ϵʽ��y=��100x+550��2.5��x��5.5����
����׳�����ʱy��x֮��ĺ�����ϵʽ��y=��100x+550��2.5��x��5.5����
��3��300��[��300��180����1.5]=3.75Сʱ����x=3.75ʱ��y=175ǧ�ף�
���ҳ�����A��ʱ�׳���A�ص�·����175ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
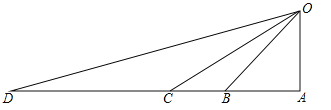
����Ŀ����һ�������硱��С��O����˽ϴ���ƻ������ֲ���Ѹ����֯�������Ӳִ�D��������Ԯ���ʣ��ƻ����������˵���D��ͬһֱ���ϵ�C��B��A������ͷ�е�һ�������û����˵�С��O����֪��OA��AD����ODA=15�㣬��OCA=30�㣬��OBA=45��CD=20km����������ʻ���ٶ�Ϊ50km/ʱ���������е��ٶ�Ϊ25km/ʱ���������������ĸ���ͷװ���������˵�С��O���������ʰ���������ÿ����ͷ����Ч����ͬ���ο����ݣ�![]() ��1.4��
��1.4��![]() ��1.7����
��1.7����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
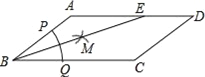
����Ŀ����ͼ����ABCD�У�AB=3��BC=5���Ե�B��Բ�ģ������ⳤΪ�뾶�������ֱ�BA��BC�ڵ�P��Q���ٷֱ���P��QΪԲ�ģ��Դ���![]() PQ�ij�Ϊ�뾶�����������ڡ�ABC�ڽ��ڵ�M������BM���ӳ���AD�ڵ�E����DE�ij�Ϊ_____��
PQ�ij�Ϊ�뾶�����������ڡ�ABC�ڽ��ڵ�M������BM���ӳ���AD�ڵ�E����DE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=3x��ͼ���뷴��������y=![]() ��ͼ���ڵ�A��1��m���͵�B��
��ͼ���ڵ�A��1��m���͵�B��
��1����m��ֵ�ͷ����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д��ʹ������������ֵ���ڷ�����������ֵ���Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
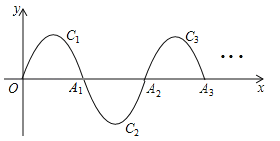
����Ŀ����ͼ��һ�������ߣ�y=��x��x��2����0��x��2����ΪC1������x�ύ������O��A1����C1��A1��ת180��õ�C2����x����A2����C2��A2��ת180��õ�C3����x����A3������˽�����ȥ��ֱ���õ�C6������P��11��m���ڵ�6��������C6�ϣ���m= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������2019��һ����������ֵ��GDP��Ϊ129 800 000 000Ԫ����129 800 000 000�ÿ�ѧ��������ʾӦΪ��������
A. 1298��108B. 1.298��108C. 1.298��1011D. 1.298��1012
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
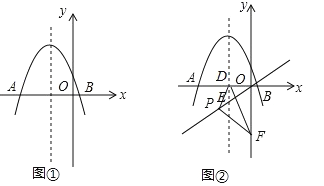
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��m��0����x�ύ�ڵ�A��B����A�ڵ�B����ࣩ���������ߵĶԳ�����ֱ��
��m��0����x�ύ�ڵ�A��B����A�ڵ�B����ࣩ���������ߵĶԳ�����ֱ��![]() �ཻ�ڵ�E����x���ཻ�ڵ�D����P��ֱ��
�ཻ�ڵ�E����x���ཻ�ڵ�D����P��ֱ��![]() �ϣ�����ԭ���غϣ�������PD������P��PF��PD��y���ڵ�F������DF��
�ϣ�����ԭ���غϣ�������PD������P��PF��PD��y���ڵ�F������DF��
��1����ͼ����ʾ���������߶����������Ϊ![]() ���������ߵĽ���ʽ��
���������ߵĽ���ʽ��
��2����A��B��������ꣻ
��3����ͼ����ʾ��С����̽����P��λ�÷��֣�����P���E�غ�ʱ����PDF�Ĵ�СΪ��ֵ���������룺����ֱ��![]() ������һ��P������ԭ���غϣ�����PDF�Ĵ�СΪ��ֵ�������жϸò����Ƿ���ȷ����˵��������
������һ��P������ԭ���غϣ�����PDF�Ĵ�СΪ��ֵ�������жϸò����Ƿ���ȷ����˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC��DE��BC��
��1��������ADE�Ƿ��ǵ��������Σ�˵�����ɣ�
��2����MΪDE�ϵĵ㣬��BMƽ�֡�ABC��CMƽ�֡�ACB������ADE���ܳ�Ϊ20��BC=8������ABC���ܳ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com