
 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | m | … |
分析 (1)由二次函数图象经过点(1,0),(3,0),设出交点式,利用待定系数法求函数解析式,进一步代入点得出答案即可;
(2)利用表中的点描点,画出函数图象即可;
(3)利用图象得出答案即可.
解答 解:(1)∵抛物线y=ax2+bx+c(a≠0)过点(1,0),(3,0),
∴可设抛物线解析式为y=a(x-1)(x-3),
∵过点(0,3),
∴a=1,
∴y=(x-1)(x-3)=x2-4x+3,
当x=4时,m=3,
∴抛物线的解析式为y=x2-4x+3,m的值为3.
(2)y=x2-4x+3=(x-2)2-1,
顶点坐标为(2,-1),与y轴的交点坐标为(0,3),
函数图象如下:
(3)由图表可知抛物线y=ax2+bx+c过点(0,3),(4,3),
因此当y<3时,x的取值范围是0<x<4.
点评 此题考查待定系数法求函数解析式,二次函数的图象,掌握待定系数法求函数解析式的方法与步骤是解决问题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
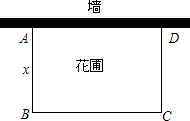 如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm.
如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知这是一座圆弧形涵洞的入口的示意图,涵洞的最高点C到地面AB的距离为6米,涵洞入口地面的宽度AB为4米,请你求这座涵洞圆弧所在圆的半径长.
如图,已知这是一座圆弧形涵洞的入口的示意图,涵洞的最高点C到地面AB的距离为6米,涵洞入口地面的宽度AB为4米,请你求这座涵洞圆弧所在圆的半径长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..
如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com