
分析 (1)利用例1中给出的方法分解因式即可;
(2)利用例2中给出的方法分解因式,进一步开方即可;
(3)分组分解,利用非负数的性质求得最小值即可.
解答 解:(1)x2-40x+319
=x2-40x+400-400+319
=(x-20)2-81
=(x-20+9)(x-20-9)
=(x-11)(x-29);
(2)$\sqrt{10-4\sqrt{6}}$
=$\sqrt{4-4\sqrt{6}+6}$
=$\sqrt{(\sqrt{6}-2)^{2}}$
=$\sqrt{6}$-2;
(3)4x2+y2-2y-4x+15
=4x2-4x+1+y2-2y+1+13
=(2x-1)2+(y-1)2+13
(2x-1)2≥0,(y-1)2≥0,
所以4x2+y2-2y-4x+15的最小值是13.
点评 此题考查配方法的运用,掌握完全平方公式是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
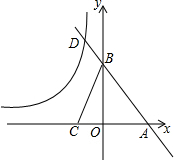 如图,直线AB与x轴、y轴分别交于点A、点B,与双曲线y=$\frac{k}{x}$(x<0)交于点D,点C在x轴上,连接CB,tanC=3,且AB=3DB,线段OA、OC(OA>OC)的长是一元二次方程x2-4x+3=0的两根.
如图,直线AB与x轴、y轴分别交于点A、点B,与双曲线y=$\frac{k}{x}$(x<0)交于点D,点C在x轴上,连接CB,tanC=3,且AB=3DB,线段OA、OC(OA>OC)的长是一元二次方程x2-4x+3=0的两根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD和正方形EFGH的对角线BD、FH都在x轴上,O、M分别为正方形ABCD和正方形EFGH的中心(正方形对角线的交点称为正方形的中心),O为平面直角坐标系的原点,OD=3,MH=2,DF=3.
如图,正方形ABCD和正方形EFGH的对角线BD、FH都在x轴上,O、M分别为正方形ABCD和正方形EFGH的中心(正方形对角线的交点称为正方形的中心),O为平面直角坐标系的原点,OD=3,MH=2,DF=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
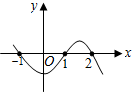 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )| A. | x<0 | B. | x<-1或1<x<2 | C. | -1<x<1或x>2 | D. | x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | m | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com