
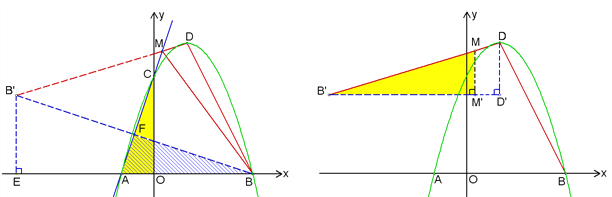
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(��2, 0), C(0, 6)�����������y����![]() x2��ax��b��x�ύ����һ��B����D�������ߵĶ��㣮
x2��ax��b��x�ύ����һ��B����D�������ߵĶ��㣮
��1����a��b��ֵ��
��2����P��x���ϵ�һ�����㣬��P��ֱ��l//AC���������ڵ�Q�����ŵ�P���˶�������A��P��Q��CΪ������ı�����ƽ���ı��Σ���ֱ��д�����������ĵ�Q�����ꣻ
(3)��ֱ��AC���Ƿ����һ��M��ʹ��BDM���ܳ���С�������ڣ����ҳ���M�������M�����꣮�������ڣ���˵�����ɡ�


����ͼ
���𰸡���1��a=2��b=6��
��2��Q(4,6)��Q![]() ��
��![]() ��
��
��3������һ��M![]() ��ʹ��BDM���ܳ���С
��ʹ��BDM���ܳ���С
�������������������1���ѵ�A��C��������뵽����ʽ�У��ô���ϵ������������a��b��ֵ��
��2�����P��t��0��������ƽ���ı��ζ����λ�ò�ȷ����������Ҫ�������ۣ�����ƽ�Ƶ����ʣ��ú�t��ʽ�ӱ�ʾ����Q���������ѵ�Q��������뵽���κ����Ľ���ʽ�У����t������Եõ���Q������.
��3������B����ֱ��AC�ĶԳƵ�B��������BB������AC�ڵ�M�����M������Ҫ��ĵ�.����B����B��E��x�ᣬ�������������εõ�B�������꣬��B��DΪֱ�ǵ�б�߹���ֱ������������ɵõ�M������.
���������(1)���������![]() ����A��-2��0�������a=2.����a=2��b=6.
����A��-2��0�������a=2.����a=2��b=6.
��2����P��t,0��,�ɣ�1���ã�A��-2��0����C��0��6��.����ƽ�Ƶ����ʵã�
��![]() ��
�� ![]() ����Q��t+2��6��������
����Q��t+2��6��������![]() ����ã�
����ã� ![]() ��
�� ![]() ���ᣩ������Q��4��6��.
���ᣩ������Q��4��6��.
��![]() ��
�� ![]() ����Q��t-2��-6��������
����Q��t-2��-6��������![]() ����ã�
����ã� ![]() ��
�� ![]() ������Q��
������Q��![]() ��-6����
��-6����![]() ��-6��.
��-6��.
��![]() ��
�� ![]() ����Q��-t-2��6��������
����Q��-t-2��6��������![]() ����ã�
����ã� ![]() ���ᣩ.
���ᣩ.
����������Q(4,6)��Q��![]() ��-6����
��-6����![]() ��-6��.
��-6��.
��3�����B����ֱ��AC�ĶԳƵ�ΪB��������BB����AC��F��
����B��D��B��D��AC�Ľ������Ҫ��ĵ�M��
��B��E��x����E����ô��BB��E�ס�BAF�ס�CAO����AO=2��CO=6����AC=![]() B(6��0)��D(2��8).
B(6��0)��D(2��8).
��Rt��BAF�� ![]()
��Rt��BB��E�� ![]()
![]() .
.
��Ϊ��M��ֱ��y��3x��6�ϣ����M������Ϊ(x, 3x��6)��
��![]() ����
����![]()
 .
.
ͼ2 ͼ3


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷�֤��֤�����������������һ��ֱ�ǻ�۽���,��һ��Ӧ����(����)
A. ��������������һ��ֱ�ǻ�۽�
B. ������������������ֱ�ǻ�۽�
C. ��������û��ֱ�ǻ�۽�
D. �������������Ƕ���ֱ�ǻ�۽�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��B��ֱ�߽���������E,����tan��EBA=
��x�ύ��A��B���㣬��B��ֱ�߽���������E,����tan��EBA=![]() ����һֻ���ϴ�A����,����1��λ/s���ٶ������߶�BE�ϵĵ�D��������1.25��λ/s���ٶ�����DE����E�㴦��ʳ�������ϴ�A��E�����ʱ����________s
����һֻ���ϴ�A����,����1��λ/s���ٶ������߶�BE�ϵĵ�D��������1.25��λ/s���ٶ�����DE����E�㴦��ʳ�������ϴ�A��E�����ʱ����________s

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ֻ�Խ��Խ�ܵ����ڵ�ϲ�������ֿ�ʽ���Ͷ���г���ij�꾭Ӫ��A���ֻ�ȥ�������ܶ�Ϊ50000Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����20%��
��1������A���ֻ�ÿ���ۼ۶���Ԫ��
��2���õ�ƻ��½�һ��A���ֻ���B���ֻ���60������B���ֻ��Ľ�������������A���ֻ�������������Ӧ��ν�������ʹ�����ֻ�������ࣿ
A��B�����ֻ��Ľ��������ۼ۸����±���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijרӪ�̳�����һ��Ʒ�Ƶ��ԣ�ÿ̨���ԵĽ�������0.4��Ԫ��ͼ�е�ֱ��l1��ʾ��Ʒ�Ƶ���һ�����������y1����Ԫ����������x��̨���Ĺ�ϵ����֪�̳�ÿ��ķ��⡢ˮ�硢���ʵȹ̶�֧��Ϊ3��Ԫ�� 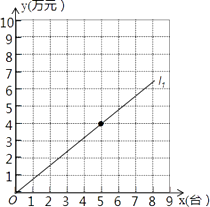
��1��ֱ��l1��Ӧ�ĺ�������ʽ�� �� ÿ̨���Ե����ۼ�����Ԫ��
��2��д���̳�һ����ܳɱ�y2����Ԫ����������x��̨��֮��ĺ�������ʽ����
��3����ͼ��ֱ������ϵ�л����ڣ�2��С���ͼ����l2����
��4��ͨ������˵����ÿ���������ﵽ����̨ʱ���̳�����ӯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��������ε�һ�����Ϊ30�㣬��ô���������εı����ǣ� ��
A.6
B.11
C.12
D.18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε����߳��ֱ�Ϊ4��7�������߳��Ƿ���x2��7x+12=0�Ľ⣬������ߵij�Ϊ�� ����
A. 3B. 4C. 3��4D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����һ��Ϊ25cm����Ϊ20cm�ij�����ӲֽƬ����һ���ǵij�������ӣ������ڳ�����ֽƬ���ĸ��Ǹ���ȥһ����ͬ��С�����Σ� 
��1������С�����εı߳�Ϊx cm���ú�x�Ĵ���ʽ��ʾͼ����Ӱ���ֵ������
��2����x=5ʱ����������ӵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У�AB��BC��AB=6��BC=4��P�ǡ�ABC�ڲ���һ�����㣬�������PAB=��PBC�����߶�CP������СֵΪ�� ��.

A. 4 B. ![]() C.
C. ![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com